Bézout's Identity
Bézout's identity states that the greatest common divisor (GCD) of two integers, \( a \) and \( b \), can be expressed as a linear combination of \( a \) and \( b \) with integer coefficients \( j \) and \( k \): $$ \gcd(a,b) = d = aj + bk $$
Finding the Coefficients in Bézout's Identity
To determine the integer coefficients \( j \) and \( k \), we can use the Euclidean algorithm, which involves repeated division.
A Practical Example
Let's compute the GCD of 2016 and 35:
$$ a = 2016 \\ b = 35 $$
Using the Euclidean algorithm:
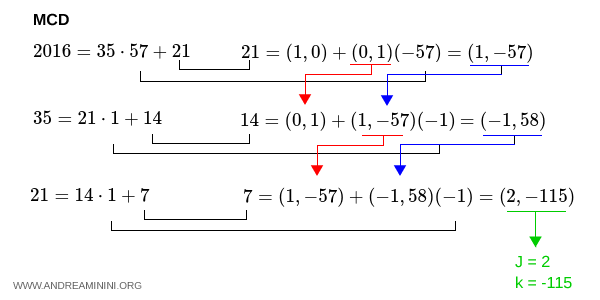
$$ 2016 = 35 \cdot 57 + 21
\\ 35 = 21 \cdot 1 + 14
\\ 21 = 14 \cdot 1 + 7
\\ 14 = 7 \cdot 2 + 0
$$
Note: The last term in each equation represents the remainder of the division.
The last nonzero remainder (7) is the greatest common divisor of 2016 and 35:
$$ \gcd(2016,35) = 7 $$
Now, to find the coefficients for Bézout’s identity, we start by assigning unit values to \( a \) and \( b \):
$$ a = (1,0) \\ b = (0,1) $$
Next, we express each remainder from the Euclidean algorithm in terms of the previous two values:
$$ r_1 = a + b(-q_1)
\\ r_2 = b + r_1(-q_2)
\\ r_3 = r_1 + r_2(-q_3)
\\ r_4 = r_2 + r_3(-q_4) \\
\vdots $$
Here, $ q_i $ is the quotient of the division.
After setting up the first equation, we progressively substitute values without recalculating them at each step.
$$ 21 = (1,0)+(0,1)(-57) = (1,0)+(0,-57) = (1,-57) $$
Explanation. In the first step of the GCD computation, $$ 2016 = 35 \cdot 57 + 21 $$ the remainder is $ r_1 = 21 $, and the quotient is $ q_1 = 57 $. Meanwhile, $ a = (1,0) $ and $ b = (0,1) $.
$$ 14 = (0,1)+(1,-57)(-1) = (0,1)+(-1,57) = (-1,58) $$
$$ 7 = (1,-57)+(-1,58)(-1) = (1,-57) + (1,-58) = (2,-115) $$
Since we’ve reached the final remainder, the last pair of values gives us the coefficients for Bézout’s identity:
$$ j = 2 \\ k = -115 $$
Thus, we can express the GCD as:
$$ \gcd(2016,35) = 7 = 2016 \cdot j + 35 \cdot k $$
$$ 2016 \cdot 2 + 35 \cdot (-115) $$
We have now written the greatest common divisor as a linear combination of 2016 and 35.
Verification: To confirm our result, let's compute the linear combination: $$ 2016 \cdot 2 + 35 \cdot (-115) \\ 4032 - 4025 = 7 $$
Example
Let’s take the following integers:
$$ a = 1869 \\ b = 1617 $$
We’ll use the Euclidean algorithm to find the greatest common divisor, $ \text{GCD}(1869, 1617) $.
$$ 1869 = 1617 \cdot 1 + 252
\\ 1617 = 252 \cdot 6 + 105
\\ 252 = 105 \cdot 2 + 42
\\ 42 = 21 \cdot 2 + 0
$$
So, the greatest common divisor is 21:
$ \text{GCD}(1869, 1617) = 21 $
We now want to find two integers $ j $ and $ k $ such that the following identity holds:
$$ a \cdot j + b \cdot k = \text{GCD}(a, b) $$
Which in this case becomes:
$$ 1869 \cdot j + 1617 \cdot k = 21 $$
To compute the coefficients $ j $ and $ k $, we start by assigning unit vectors to $ a $ and $ b $:
$$ a = (1, 0), \quad b = (0, 1) $$
We then express each remainder in the division sequence as a linear combination of $ a $ and $ b $, using the recursive formula: $ r_i = r_{i-2} + (-q_i) \cdot r_{i-1} $. Here, $ r_{i-2} $ and $ r_{i-1} $ are represented by ordered pairs, starting with $ a = (1, 0) $ and $ b = (0, 1) $.
$$ 252 = (1, 0) + (-1) \cdot (0, 1) = (1, -1) $$
$$ 105 = (0, 1) + (-6) \cdot (1, -1) = (-6, 7) $$
$$ 42 = (1, -1) + (-2) \cdot (-6, 7) = (13, -15) $$
$$ 21 = (-6, 7) + (-2) \cdot (13, -15) = (-32, 37) $$
Therefore, the coefficients that satisfy the identity are $ j = -32 $ and $ k = 37 $:
$$ 1869 \cdot (-32) + 1617 \cdot 37 = 21 $$
Verification. Let’s perform the arithmetic to confirm the result: $$ -59808 + 59829 = 21 $$ $$ 21 = 21 $$ The identity is verified.
And that’s it!
