Congruences in Modular Arithmetic

Two integers \( a \) and \( b \), with \( b > 0 \), are said to be congruent modulo \( n \) if their difference \( a - b \) is divisible by a positive integer \( n \). $$ a \equiv b \mod n $$

Another way to express this is:

Two integers \( a \) and \( b \) (\( b > 0 \)) are congruent modulo \( n \) (\( n > 0 \)) if they leave the same remainder when divided by \( n \). $$ a \equiv b \mod n $$

Simply put, modular congruence means that two numbers, \( a \) and \( b \), yield the same remainder when divided by \( n \).

These two definitions are equivalent—if one holds, the other follows automatically.

In number theory, congruences extend the concept of equality to integers by considering their behavior under division by a fixed value, known as the modulus.

Example. Consider three integers: \( a = 17 \), \( b = 5 \), and \( n = 6 \) (where \( n > 0 \)). We say that \( a \) is congruent to \( b \) modulo \( n \), written as $$ a \equiv b \pmod{n} $$ if and only if the difference \( a - b \) is a multiple of \( n \). In other words, if there exists an integer \( k \) such that \( a - b = kn \). To verify this, we compute: $$ 17 - 5 = 12 $$ Since \( 12 \) is a multiple of \( n = 6 \) (because \( 12 = 2 \times 6 \)), we conclude that 17 and 5 are congruent modulo 6. $$ 17 \equiv 5 \pmod{6} $$ This means that when both \( 17 \) and \( 5 \) are divided by \( 6 \), they leave the same remainder \( r \). $$ 17 \div 6 = 2 \ \ r=5 $$ $$ 5 \div 6 = 0 \ \ r=5 $$

Thus, congruence defines an equivalence relation among integers, grouping them based on their remainders when divided by a positive integer \( n \).

$$ a \: p_n \: b \Leftrightarrow a \equiv b \mod n \Leftrightarrow a-b=n \cdot k $$

where \( k \) is any integer. 

A Practical Example

Method 1

Let’s look at a simple example:

$$ 26 \equiv 16 \mod 5 $$

because

$$ 26 - 16 = 10 $$

and 10 is divisible by 5.

This means that when divided by 5, both numbers leave the same remainder:

$$ 26 \div 5 = 5 \ \ r=1 $$

$$ 16 \div 5 = 3 \ \ r=1 $$

Method 2

We can verify the same congruence using a different approach:

$$ 26 \equiv 16 \mod 5 $$

because

$$ 26 \div 5 = 5 \text{ remainder } 1 $$

$$ 16 \div 5 = 3 \text{ remainder } 1 $$

Since both numbers give a remainder of 1 when divided by 5, we confirm that \( 26 \) and \( 16 \) are congruent modulo 5.

Example 3

The result remains valid even when \( a < b \).

For instance, let’s take \( a = 5 \), \( b = 8 \), and \( n = 6 \).

In this case, the difference is negative:

$$ a - b = 5 - 8 = -3 $$

Since \( -3 \) is not a multiple of \( 6 \), meaning there is no integer \( k \) such that \( 6 \times k = -3 \), we conclude that the two numbers are not congruent modulo \( 6 \).

$$ 5 \not \equiv 8 \pmod{6} $$

Alternatively, we could verify this by checking the remainders of both numbers when divided by \( 6 \).

$$ 5 \div 6 = 0 \text{ remainder } 5 $$

$$ 8 \div 6 = 1 \text{ remainder } 2 $$

Since the remainders are different, we confirm that \( 5 \not \equiv 8 \pmod{6} \). 

Why Are Congruences Useful?

Congruences provide a way to connect the infinite set of integers to a finite set known as the quotient set modulo \( m \).

Note. Many scientific fields (mathematics, computer science, etc.) rely on the set of integers \( \mathbb{Z} \). However, working with an infinite set can be cumbersome. Congruences allow us to simplify things by mapping integers onto a finite set, making computations much more manageable.

Example

Consider two sets:

- Set \( A \), which consists of the positive integers \( \mathbb{Z}^+ \) and is infinite.

- Set \( B \), which is finite and contains only the numbers 1, 2, and 3.

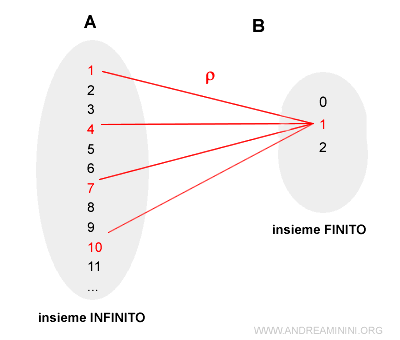
An equivalence relation \( p \) associates each element of \( A \) with a corresponding element in \( B \).

For instance, the number 4 in \( A \) is congruent modulo 3 to the number 1 in \( B \) because both leave the same remainder when divided by \( m = 3 \).

$$ 4 \div 3 = 1 \text{ remainder } 1 $$

$$ 1 \div 3 = 0 \text{ remainder } 1 $$

The same holds for 7 in \( A \):

$$ 7 \div 3 = 2 \text{ remainder } 1 $$

$$ 1 \div 3 = 0 \text{ remainder } 1 $$

And for 10 in \( A \):

$$ 10 \div 3 = 3 \text{ remainder } 1 $$

$$ 1 \div 3 = 0 \text{ remainder } 1 $$

This pattern continues for all numbers in \( A \) of the form \( 1 + 3n \).

In summary, every integer in set \( A \) belongs to a specific subset within \( B \), forming what is known as an equivalence class.

What Are the Practical Applications? Congruences have numerous real-world applications. In cryptography, they are essential for the RSA encryption system, which secures digital communication. They also play a key role in modular arithmetic, helping analyze integer sets in cyclic patterns and solve problems involving integer solutions.

The Quotient Set Modulo \( n \)

In the previous example, we established a congruence relation modulo 3.

The equivalence classes in this relation are:

$$ \bar{0} = \{ 3, 6, 9, 12, ... \} \\ \bar{1} = \{ 1, 4, 7, 10, ... \} \\ \bar{2} = \{ 2, 5, 8, 11, ... \} $$

The set of these equivalence classes is called the quotient set modulo \( n \).

$$ \mathbb{Z}_n = \{ \bar{0}, \bar{1}, \bar{2} \} $$

The quotient set modulo \( n \) consists of \( n \) elements, starting from zero.

Thus, the classes range from 0 to \( n-1 \).

Operations on Congruences

To turn a quotient set modulo \( n \) into a ring, we introduce two operations: $$ ( \mathbb{Z}_n, +, \cdot ) $$

The fundamental operations on congruences are:

• Addition: $$ \bar{a} + \bar{b} = \overline{a+b} $$
• Multiplication: $$ \bar{a} \cdot \bar{b} = \overline{ab} $$

Example

The addition and multiplication tables for the ring \( (\mathbb{Z}_6, +, \cdot) \) are shown below:

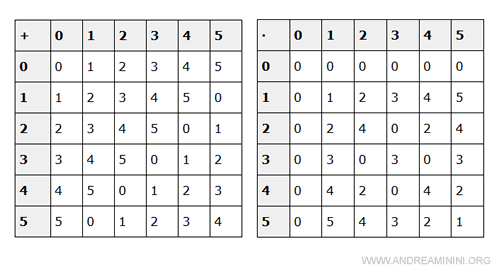
The congruence relation is compatible with both addition and multiplication as defined on the set of integers.

In other words, the validity of the relation does not depend on the specific integer representatives chosen.

If the following congruences hold:

$$ a \equiv b \pmod{n} $$

$$ c \equiv d \pmod{n} $$

then the congruence also holds for their sum and product:

$$ a + c \equiv b + d \pmod{n} $$

$$ ac \equiv bd \pmod{n} $$

Proof. If \( a \equiv b \pmod{n} \), then \( a - b = kn \) for some integer \( k \). Similarly, if \( c \equiv d \pmod{n} \), then \( c - d = jn \) for some integer \( j \). Adding these equations:

$$ (a - b) + (c - d) = kn + jn $$

$$ (a + c) - (b + d) = n(k + j) $$

Since \( (a + c) - (b + d) \) is a multiple of \( n \), we conclude that \( (a + c) \equiv (b + d) \pmod{n} \).

Example

Consider the following congruences:

$$ 7 \equiv 1 \pmod{6} \\ 8 \equiv 2 \pmod{6} $$

For addition:

$$ 7 + 8 \equiv 1 + 2 \pmod{6} $$

$$ 15 \equiv 3 \pmod{6} $$

Verification. When 15 is divided by 6, the remainder is 3. Likewise, dividing 3 by 6 also leaves a remainder of 3. Therefore, 15 and 3 are congruent modulo 6.

For multiplication:

$$ 7 \cdot 8 \equiv 1 \cdot 2 \pmod{6} $$

$$ 56 \equiv 2 \pmod{6} $$

Verification. When 56 is divided by 6, the remainder is 2. Similarly, dividing 2 by 6 leaves a remainder of 2. Thus, 56 and 2 are congruent modulo 6.

Divisibility and Congruence

A number \( a \) is divisible by \( m \) if and only if: $$ a \equiv 0 \pmod{m} $$

Example

Is 26 divisible by 13?

Using congruence properties:

$$ 26 \equiv 0 \pmod{13} $$

$$ 26 - 0 = 26 $$

Since 26 is a multiple of 13, the answer is yes.

Properties of Congruences

Congruences satisfy the following fundamental properties:

• Reflexivity: Every number is congruent to itself: $$ a \equiv a \pmod{n} $$
• Symmetry: If $$ a \equiv b \pmod{n}, $$ then $$ b \equiv a \pmod{n}. $$
• Transitivity: If $$ a \equiv b \pmod{n} $$ and $$ b \equiv c \pmod{n}, $$ then $$ a \equiv c \pmod{n}. $$
• Compatibility with algebraic operations: If $$ a \equiv b \pmod{n} $$ and $$ c \equiv d \pmod{n}, $$ then the following also hold: $$ a + c \equiv b + d \pmod{n}, $$ $$ a - c \equiv b - d \pmod{n}, $$ $$ ac \equiv bd \pmod{n}. $$

Additional Properties of Congruences

Congruences also obey the following rules:

• Congruences with the same modulus can be combined through addition, subtraction, and multiplication: $$ a \equiv b \pmod{m}, \quad c \equiv d \pmod{m} \Rightarrow a + c \equiv b + d \pmod{m} $$ $$ a \equiv b \pmod{m}, \quad c \equiv d \pmod{m} \Rightarrow a - c \equiv b - d \pmod{m} $$ $$ a \equiv b \pmod{m}, \quad c \equiv d \pmod{m} \Rightarrow ac \equiv bd \pmod{m} $$
• A congruence can be multiplied by any integer \( k \): $$ k \cdot ( a \equiv b \pmod{m} ) \Rightarrow ka \equiv kb \pmod{m} $$
• Repeating the same congruence results in a power relation: $$ ( a \equiv b \pmod{m} ) \cdot ( a \equiv b \pmod{m} ) \Rightarrow a^2 \equiv b^2 \pmod{m} $$
• For any integer \( c \), the following hold: $$ a + c \equiv b + c \pmod{n}, $$ $$ ac \equiv bc \pmod{n}, $$ $$ a^c \equiv b^c \pmod{n}. $$
• If \( a \equiv b \pmod{n} \) and \( d \) is a divisor of \( n \), then: $$ a \equiv b \pmod{d}. $$

  Example. The numbers 15 and 21 are congruent modulo 6: $$ 15 \equiv 21 \pmod{6}. $$ Choosing a divisor \( 2 \) (since \( 2 \mid 6 \)), we check their congruence modulo 2. Since both \( 15 \div 2 \) and \( 21 \div 2 \) leave a remainder of 1, we conclude: $$ 15 \equiv 21 \pmod{2}. $$ The same holds for \( 3 \mid 6 \) since both \( 15 \div 3 \) and \( 21 \div 3 \) leave a remainder of 0: $$ 15 \equiv 21 \pmod{3}. $$

• For two congruences: $$ a \equiv b \pmod{r}, \quad a \equiv b \pmod{s} \Rightarrow a \equiv b \pmod{\operatorname{lcm}(r,s)}. $$
• For two congruences involving a common factor: $$ ac \equiv bc \pmod{n} \Rightarrow a \equiv b \pmod{n / \gcd(c, n)}. $$
• If \( \gcd(c, n) = 1 \), then: $$ ac \equiv bc \pmod{n} \Rightarrow a \equiv b \pmod{n}. $$
• Every integer \( a \) is congruent modulo \( n \) to a unique integer \( r \) such that \( 0 \leq r < n \): $$ a \equiv r \pmod{n}. $$

  Proof. The remainder \( r \) from dividing \( a \) by \( n \) must be between 0 and \( n-1 \). If it were greater than or equal to \( n \), it would still be divisible by \( n \) and wouldn't be a remainder.

• For any integers \( a, b \) and a prime \( p \), the following holds: $$ (a + b)^p \equiv a^p + b^p \pmod{p}. $$

More Practical Examples

Example 1

Which number is congruent to \( 13 \mod 3 \)?

To find the number congruent to \( 13 \mod 3 \), we compute the remainder when \( 13 \) is divided by \( 3 \).

$$ 13 \div 3 = 4 \quad \text{with remainder } r = 1 $$

Since the remainder is \( 1 \), we conclude:

$$ 13 \equiv 1 \mod{3} $$

This means that \( 13 \) and \( 1 \) belong to the same residue class modulo \( 3 \) because they leave the same remainder when divided by \( 3 \).

Example 2

In some cases, calculating the remainder directly can be challenging.

For instance, in the following congruence, the exponent \( 12^{38} \) is extremely large:

$$ 12^{38} \mod{7} $$

To simplify the computation, we use modular exponentiation and successive reductions.

• Compute \( 12^1 \): $$ 12^1 \mod 7 = 5 $$ Since \( 12 \div 7 = 1 \) with a remainder of \( 5 \), we obtain: $$ 12^1 \equiv 5 \mod 7 $$
• Compute \( 12^2 \): $$ 12^2 \mod 7 = ( 12^1 \cdot 12^1 ) \mod 7 $$ Since \( 12^1 \equiv 5 \mod 7 \), we get: $$ 12^2 \mod 7 = ( 5 \cdot 5 ) \mod 7 = 25 \mod 7 = 4 $$
• Compute \( 12^4 \): $$ 12^4 \mod 7 = ( 12^2 \cdot 12^2 ) \mod 7 $$ Since \( 12^2 \equiv 4 \mod 7 \), we obtain: $$ 12^4 \mod 7 = ( 4 \cdot 4 ) \mod 7 = 16 \mod 7 = 2 $$
• Compute \( 12^8 \): $$ 12^8 \mod 7 = ( 12^4 \cdot 12^4 ) \mod 7 $$ Since \( 12^4 \equiv 2 \mod 7 \), we get: $$ 12^8 \mod 7 = ( 2 \cdot 2 ) \mod 7 = 4 \mod 7 = 4 $$
• Compute \( 12^{16} \): $$ 12^{16} \mod 7 = ( 12^8 \cdot 12^8 ) \mod 7 $$ Since \( 12^8 \equiv 4 \mod 7 \), we obtain: $$ 12^{16} \mod 7 = ( 4 \cdot 4 ) \mod 7 = 16 \mod 7 = 2 $$
• Compute \( 12^{32} \): $$ 12^{32} \mod 7 = ( 12^{16} \cdot 12^{16} ) \mod 7 $$ Since \( 12^{16} \equiv 2 \mod 7 \), we get: $$ 12^{32} \mod 7 = ( 2 \cdot 2 ) \mod 7 = 4 \mod 7 = 4 $$

Now, using modular exponentiation properties, we rewrite:

$$ 12^{38} = 12^{32} \cdot 12^4 \cdot 12^2 $$

Thus, the original congruence becomes:

$$ 12^{38} \mod{7} = ( 12^{32} \cdot 12^4 \cdot 12^2 ) \mod{7} $$

We already know:

• \( 12^{32} \mod 7 = 4 \)
• \( 12^4 \mod 7 = 2 \)
• \( 12^2 \mod 7 = 4 \)

Substituting these values:

$$ 12^{38} \mod{7} = ( 4 \cdot 2 \cdot 4 ) \mod{7} $$

$$ 12^{38} \mod{7} = 32 \mod{7} $$

Since:

$$ 32 \div 7 = 4 \quad \text{with remainder } r = 4 $$

We conclude:

$$ 12^{38} \mod{7} = 4 $$

Example 3 (Alternative Approach)

Another way to solve a congruence with a large exponent is to determine the smallest exponent \( x \) such that:

$$ a^x \equiv 1 \mod m $$

This value is known as the order of \( a \) modulo \( m \).

For example, let's solve the following congruence:

$$ 12^{38} \mod{7} $$

First, we observe that \( 12 \equiv 5 \mod 7 \), allowing us to simplify the calculation:

$$ 5^{38} \mod{7} $$

Next, we find the smallest \( x \) such that:

$$ 5^x \equiv 1 \mod 7 $$

Calculating successive powers of \( 5 \) modulo \( 7 \):

$$ 5^1 \equiv 5 \mod 7 $$

$$ 5^2 \equiv 25 \equiv 4 \mod 7 $$

$$ 5^3 \equiv 5^1 \cdot 5^2 \equiv 5 \cdot 4 \equiv 20 \equiv 6 \mod 7 $$

$$ 5^4 \equiv 5^2 \cdot 5^2 \equiv 4 \cdot 4 \equiv 16 \equiv 2 \mod 7 $$

$$ 5^5 \equiv 5^3 \cdot 5^2 \equiv 6 \cdot 4 \equiv 24 \equiv 3 \mod 7 $$

$$ 5^6 \equiv 5^3 \cdot 5^3 \equiv 6 \cdot 6 \equiv 36 \equiv 1 \mod 7 $$

Since \( 5^6 \equiv 1 \mod 7 \), the order of \( 5 \) modulo \( 7 \) is 6.

Note. Since 7 is a prime number and 5 and 7 are coprime integers, we can also use Fermat’s Little Theorem, which states:

$$ a^{p-1} \equiv 1 \mod p $$

For \( p = 7 \) and \( a = 5 \), we have:

$$ 5^{7-1} \equiv 1 \mod 7 $$

$$ 5^6 \equiv 1 \mod 7 $$

This confirms that the order of \( 5 \) modulo \( 7 \) is 6, providing the result more efficiently.

Now, we use this to simplify the exponent \( 38 \) in terms of the order \( 6 \):

$$ 5^{38} \mod 7 $$

$$ (5^6)^6 \cdot 5^2 \mod 7 $$

Since \( 5^6 \equiv 1 \mod 7 \), we substitute:

$$ (1)^6 \cdot 5^2 \mod 7 $$

$$ 5^2 \mod 7 $$

At this point, the computation becomes straightforward:

$$ 5^2 \equiv 4 \mod 7 $$

Thus, the final result is:

$$ 12^{38} \equiv 5^{38} \equiv 4 \mod 7 $$

This matches the result obtained in the previous example.

Example 4 (Chinese Remainder Theorem)

When the modulus is a composite number, we can apply the Chinese Remainder Theorem (CRT).

$$ 2^{85} \mod 91 $$

Since \( 91 = 13 \cdot 7 \) is a composite number, we can factorize it and compute \( 2^{85} \) modulo 7 and modulo 13 separately.

$$ 2^{85} \mod 7 $$

$$ 2^{85} \mod 13 $$

We solve these congruences independently.

1] Computing modulo 7

Since 7 is a prime and 85 is coprime to 7, we can apply Fermat’s Little Theorem, which states that \( a^{p-1} \equiv 1 \mod p \).

$$ 2^{7-1} \equiv 1 \mod 7 $$

$$ 2^6 \equiv 1 \mod 7 $$

Since \( 85 = 6 \cdot 14 + 1 \), we rewrite:

$$ 2^{85} \equiv (2^6)^{14} \cdot 2^1 \mod 7 $$

Since \( 2^6 \equiv 1 \mod 7 \), we substitute:

$$ 1^{14} \cdot 2^1 \equiv 2 \mod 7 $$

Thus,

$$ 2^{85} \equiv 2 \mod 7 $$

2] Computing modulo 13

Applying Fermat’s Little Theorem for \( p = 13 \):

$$ 2^{13-1} \equiv 1 \mod 13 $$

$$ 2^{12} \equiv 1 \mod 13 $$

Since \( 85 = 12 \cdot 7 + 1 \), we rewrite:

$$ 2^{85} \equiv (2^{12})^7 \cdot 2^1 \mod 13 $$

Since \( 2^{12} \equiv 1 \mod 13 \), we substitute:

$$ 1^7 \cdot 2^1 \equiv 2 \mod 13 $$

Thus,

$$ 2^{85} \equiv 2 \mod 13 $$

3] Solving using the Chinese Remainder Theorem

We now solve the system of congruences:

$$ \begin{cases} x \equiv 2 \mod 7 \\ x \equiv 2 \mod 13 \end{cases} $$

Since both congruences yield the same remainder, the solution is simply:

$$ x \equiv 2 \mod 91 $$

Thus, the final result is:

$$ 2^{85} \equiv 2 \mod 91 $$

And so on.