Eudoxus-Archimedes Postulate

Given two homogeneous magnitudes that are neither congruent nor zero, there exists a natural number n such that the smaller magnitude eventually exceeds the larger one.

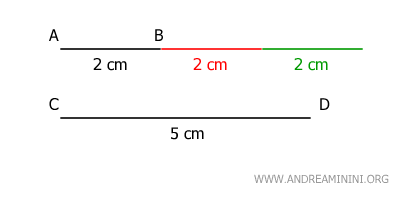
If we take two homogeneous magnitudes (measured in the same units) that are not congruent (having different measures) and non-zero, then there exists a multiple of the smaller magnitude that will exceed the larger one.

In simpler terms, the postulate states that you can always add enough copies of the smaller magnitude to surpass the larger one.

Note: This postulate was independently formulated by the Greek mathematicians Eudoxus of Cnidus and Archimedes of Syracuse. It is also known as Archimedes' Principle or Eudoxus' Principle.

A Practical Example

Consider two line segments, AB and CD.

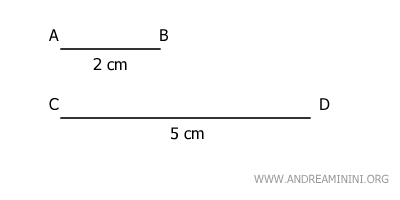
The length of segment AB is 2 cm, while the length of segment CD is 5 cm.

Clearly, the smaller magnitude is segment AB.

In this case, multiplying AB by n=3 results in a length that exceeds CD.

$$ 3 \cdot \overline{AB} > \overline{CD} $$

$$ 3 \cdot 2 \ cm > 5 \ cm $$

$$ 6 \ cm > 5 \ cm $$

In other words, adding two more copies of segment AB is enough to surpass the length of segment CD.

Additional Remarks

Here are some additional notes and observations about the postulate:

• The Eudoxus-Archimedes Principle is often viewed as a precursor to the concept of a limit, which is fundamental in calculus, both integral and differential.
• The Eudoxus-Archimedes Principle is also closely related to measure theory and integration, as it forms the basis for Riemann sums, which are essential in defining the Riemann integral.

  Note: It is remarkable how mathematical concepts developed thousands of years ago continue to play a central role in modern mathematical theory.

And so on.