Cartesian Equation of a Sphere

A sphere is the set of points P in 3D space (R3) that are equidistant from a central point C, called the center of the sphere. The distance from any point to the center is known as the radius, r. $$ d(C,P)=r $$

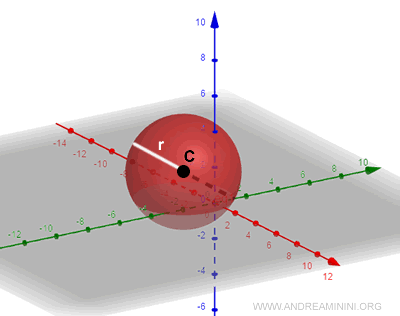
• Interior Points
  Points whose distance from the center is between 0 and r are called interior points of the sphere. $$ 0 < d(C,P) < r $$
• Exterior Points
  Points where the distance d(C,P) > r are known as exterior points of the sphere. $$ d(C,P) > r $$

Note. If the distance is zero, the sphere reduces to a single point, C.

How to Derive the Cartesian Equation of a Sphere

The definition of a sphere allows us to derive its Cartesian equation.

$$ d(C,P)=r $$

Let’s establish a Cartesian reference frame RC(O;i,j,k).

The center C is a point with coordinates x₀, y₀, z₀ in Euclidean space.

$$ C = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Now, consider a general point P on the sphere:

$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

The distance between these two points is given by:

$$ d(C,P) = \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} $$

Since the distance d(C,P) equals the radius r, we have:

$$ d(C,P) = r $$

This leads to:

$$ \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} = r $$

Squaring both sides gives us:

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

This is the standard form of the Cartesian equation of a sphere:

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Each sphere has a unique equation in this form.

To derive the full Cartesian equation of a sphere, we can expand this standard equation:

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Expanding each term, we get:

$$ (x^2 - 2xx_0 + x_0^2) + (y^2 - 2yy_0 + y_0^2) + (z^2 - 2zz_0 + z_0^2) = r^2 $$

Or:

$$ x^2 - 2xx_0 + x_0^2 + y^2 - 2yy_0 + y_0^2 + z^2 - 2zz_0 + z_0^2 - r^2 = 0 $$

We can then group the coefficients like this:

$$ \begin{pmatrix} a = -2x_0 \\ b = -2y_0 \\ c = -2z_0 \\ d = x_0^2 + y_0^2 + z_0^2 - r^2 \end{pmatrix} $$

Note. This system can also be useful for determining the radius and the unknown values from the coefficients. After a few algebraic steps, it becomes: $$ \begin{pmatrix} x_0 = - \frac{a}{2} \\ y_0 = - \frac{b}{2} \\ z_0 = - \frac{c}{2} \\ r = \sqrt{x_0^2 + y_0^2 + z_0^2 - d} \end{pmatrix} $$ The expression under the square root must be non-negative. Therefore, the condition for the equation to represent a sphere is $$ x_0^2 + y_0^2 + z_0^2 - d \geq 0 $$ or, by substituting the unknowns with the coefficients: $$ \left( \frac{a}{2} \right)^2 + \left( \frac{b}{2} \right)^2 + \left( \frac{c}{2} \right)^2 - d \geq 0 $$.

Now, substituting the coefficients into the previous equation, we obtain the general form of the Cartesian equation of a sphere:

$$ x^2 + y^2 + z^2 + ax + by + cz + d = 0 $$

As mentioned earlier, each sphere has its own unique Cartesian equation.

A Practical Example

Let's determine whether the following Cartesian equation represents a sphere:

$$ x^2 + y^2 + z^2 + 3x + 2y - 3z - 4 = 0 $$

The coefficients are:

$$ \begin{pmatrix} a = 3 \\ b = 2 \\ c = -3 \\ d = -4 \end{pmatrix} $$

It represents a sphere if the following condition holds:

$$ \left( \frac{a}{2} \right)^2 + \left( \frac{b}{2} \right)^2 + \left( \frac{c}{2} \right)^2 - d \geq 0 $$

Substituting the values of a, b, c, and d:

$$ \left( \frac{3}{2} \right)^2 + \left( \frac{2}{2} \right)^2 + \left( \frac{-3}{2} \right)^2 - (-4) \geq 0 $$

$$ \frac{9}{4} + 1 + \frac{9}{4} + 4 \geq 0 $$

$$ \frac{9}{2} + 5 \geq 0 $$

$$ \frac{19}{2} \geq 0 $$

The expression is non-negative, so it represents a sphere.

How to Find the Center and Radius of the Sphere

Once we've determined that it’s a sphere, we can calculate the coordinates of the center C ( x₀, y₀, z₀ ) and the radius r.

The system is:

$$ \begin{pmatrix} a = -2x_0 \\ b = -2y_0 \\ c = -2z_0 \\ d = x_0^2 + y_0^2 + z_0^2 - r^2 \end{pmatrix} $$

Substituting the values of a, b, c, and d, we get:

$$ \begin{pmatrix} 3 = -2x_0 \\ 2 = -2y_0 \\ -3 = -2z_0 \\ -4 = x_0^2 + y_0^2 + z_0^2 - r^2 \end{pmatrix} $$

This gives us:

$$ x_0 = - \frac{3}{2}, \, y_0 = -1, \, z_0 = \frac{3}{2} $$

The radius is:

$$ r^2 = x_0^2 + y_0^2 + z_0^2 + 4 $$

So:

$$ r = \sqrt{ \left( - \frac{3}{2} \right)^2 + (-1)^2 + \left( \frac{3}{2} \right)^2 + 4 } $$

$$ r = \sqrt{ \frac{9}{4} + 1 + \frac {9}{4} + 4 } $$

$$ r = \sqrt{ \frac{9}{2} + 5 } $$

$$ r \approx 3.08 $$

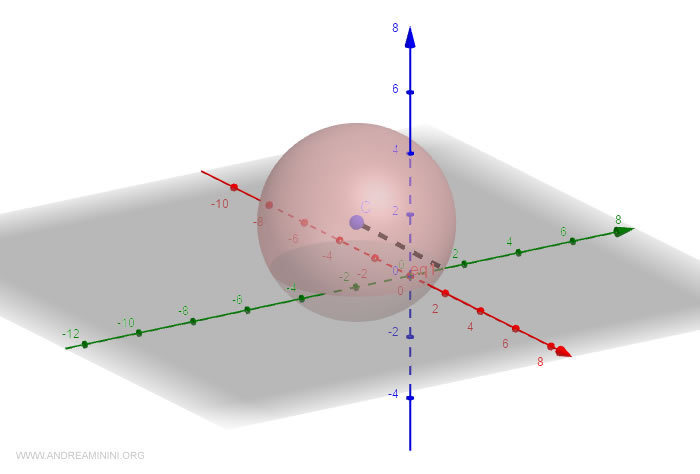
Thus, the coordinates of the center are:

$$ C = \begin{pmatrix} - \frac{3}{2} \\ -1 \\ \frac{3}{2} \end{pmatrix} $$

And the radius is:

$$ r = 3.08 $$

Note. I have verified the coordinates of the center and the radius of the sphere using Geogebra, and the calculations are correct.

And so on