Plane Intersecting, Tangent, or External to a Sphere

A plane α can either intersect, be tangent to, or lie outside a sphere with center C and radius r, depending on whether the distance between the plane and the sphere's center is less than, equal to, or greater than the radius. $$d(C,\alpha) < r \:\: intersecting \\ d(C,\alpha) = r \:\: tangent \\ d(C,\alpha) > r \:\: external$$

A Practical Example

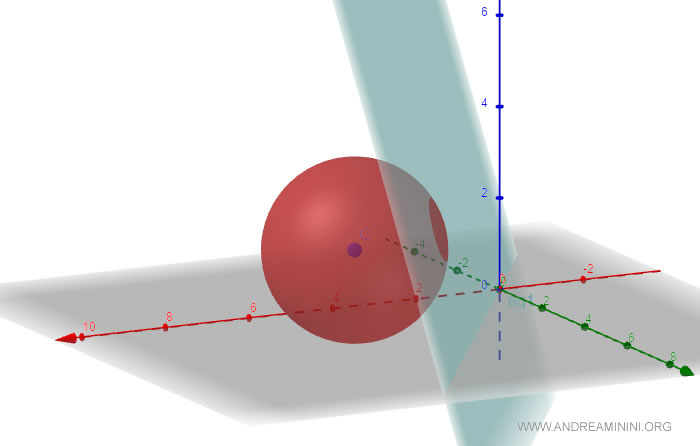
Consider a sphere with center C at coordinates (x, y, z) in space, and a radius of 2.

$$C = \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix}$$

$$r = 2$$

Now, let's define a plane α in space as follows:

$$\alpha : -3x + 2y + z = 0$$

We want to determine whether this plane intersects, is tangent to, or lies outside the sphere.

To do this, we calculate the distance between the center C of the sphere and the plane.

$$d(C,\alpha) = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}}$$

Substituting the values from the equation of the plane:

$$d(C,\alpha) = \frac{|-3x_0 + 2y_0 + z_0 + d|}{\sqrt{(-3)^2 + 2^2 + 1^2}}$$

$$d(C,\alpha) = \frac{|-3(5) + 2(3) + 1(2) + 0|}{\sqrt{9 + 4 + 1}}$$

$$d(C,\alpha) = \frac{|-15 + 6 + 2|}{\sqrt{14}}$$

$$d(C,\alpha) = \frac{7}{\sqrt{14}} \approx 1.87$$

The distance between the plane and the sphere's center is less than the radius:

$$d(C,\alpha) \approx 1.87 < r = 2$$

Therefore, the plane intersects the sphere.

And so forth.