Points Inside and Outside the Sphere

In relation to the sphere, points can be classified as follows:

• Internal points if the distance from point P to the center C of the sphere is less than the radius r. $$ d(C,P) < r $$
• External points if the distance from point P to the center C of the sphere is greater than the radius r. $$ d(C,P) > r $$

A Practical Example

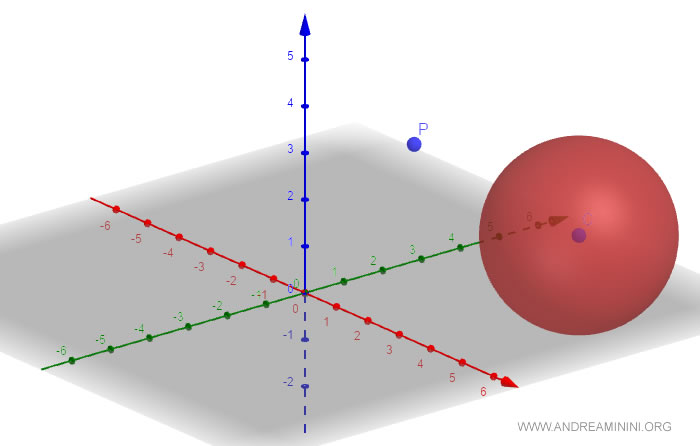
Let’s consider a sphere with its center at coordinates (x, y, z) in space and a radius of two.

$$ C = \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix} $$

$$ r = 2 $$

Now, let’s take a point P in space with the following coordinates:

$$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$

We need to determine whether this point is inside or outside the sphere.

To do this, we calculate the distance between the two points, CP.

$$ ||\overrightarrow{CP}|| = \sqrt{(5-1)^2+(3-2)^2+(2-3)^2} $$

$$ ||\overrightarrow{CP}|| = \sqrt{(4)^2+(1)^2+(1)^2} $$

$$ ||\overrightarrow{CP}|| = \sqrt{18} \approx 4.24 $$

The distance between points C and P is approximately 4.24, which is greater than the radius of the sphere, r=2.

$$ d(C,P)=4.24 > r = 2 $$

Thus, point P lies outside the sphere.

And that’s how it works.