Planes
A plane is a fundamental concept in geometry characterized by two dimensions: length and width.
A plane extends infinitely in all directions and has no thickness or boundaries.
It is usually represented by a letter from the Greek alphabet (e.g., α, β, γ, δ, etc.).
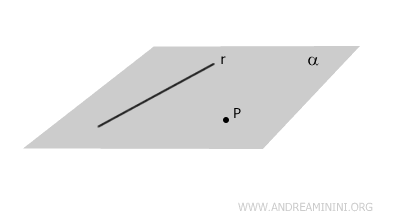
When a line or point lies on a plane, it is said to belong to the plane.
For example, line r belongs to plane alpha.
How is a Plane Defined?
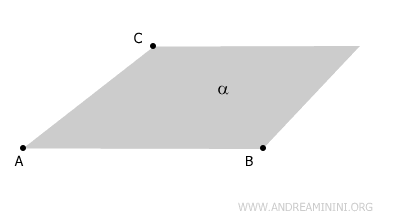
A plane is defined by three non-collinear points (A, B, C) because exactly one plane α passes through any three non-collinear points.
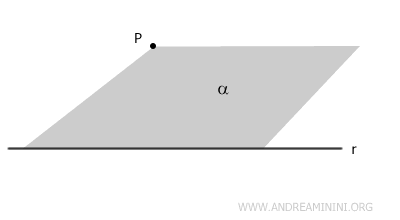
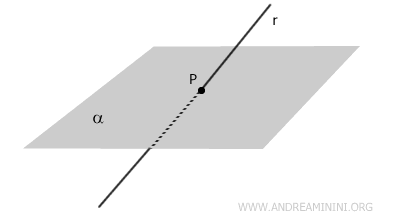
Alternatively, a plane can also be defined by a line and a point not on that line.
For a line r and a point P not on the line, there is exactly one plane α that contains both.
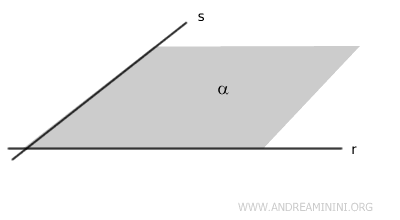
Finally, a plane can also be defined by two intersecting lines.
Through two intersecting lines r and s, there is exactly one plane α.
The Half-Plane
A half-plane is a portion of a plane divided by a line.
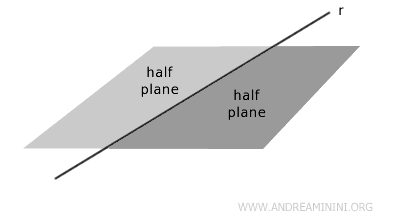
In other words, when a line is drawn on a plane, it divides the plane into two distinct parts, each of which is a half-plane.
Intersecting and Parallel Planes
Depending on their position in space, two distinct planes are either intersecting or parallel.
- Intersecting Planes
Two planes intersect if they share exactly one line.
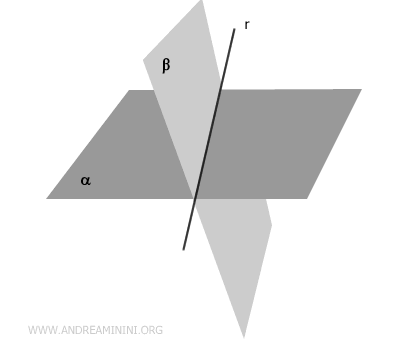
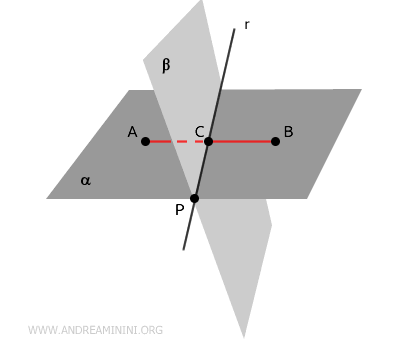
Theorem. If two distinct planes $ \alpha $ and $ \beta $ intersect at a point $ P \in \alpha \cap \beta $, they share a common line $ r $ that passes through that point. $$ \exists \ r \ | \ P \in r, r \in \alpha \cap \beta $$
- Parallel Planes
Two planes are parallel if they have no points in common (non-coincident parallel planes) or all points in common (coincident planes).
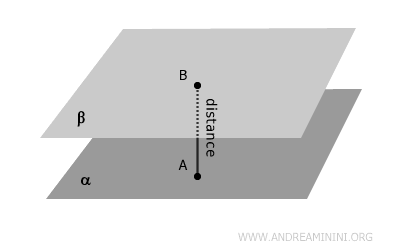
The distance between two parallel planes is the length of the segment perpendicular to both planes that connects a point on each plane.
The relationship of parallelism between planes has reflexive, symmetric, and transitive properties.
- Reflexive Property
Every plane is parallel to itself $$ \alpha || \alpha $$ - Symmetric Property
If plane α is parallel to plane β, then plane β is parallel to plane α $$ \alpha || \beta \Leftrightarrow \beta || \alpha $$ - Transitive Property
If plane α is parallel to plane β and plane β is parallel to plane γ, then plane α is parallel to plane γ $$ \alpha || \beta \ , \ \beta || \gamma \Rightarrow \alpha || \gamma $$
The Position of a Line in the Plane
A line in the plane can be:
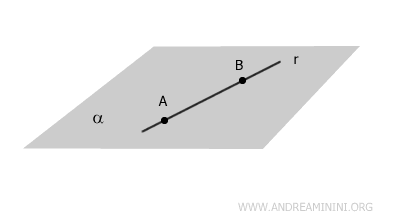
- Coplanar Line (or lying on the plane)
The line lies on the plane. All points on the line are also on the plane r⋂α=r.
- Intersecting Line
The line and the plane share exactly one point r⋂α={P}. An intersecting line can be perpendicular or oblique to the plane.
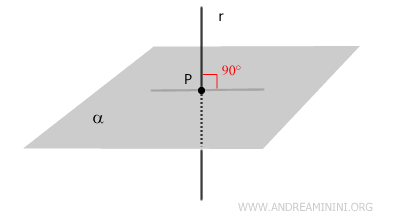
- Line Perpendicular to a Plane
If the line is perpendicular to every line in the plane that passes through the point of intersection (called the foot of the perpendicular).
- Oblique Line
If the line is not perpendicular to the plane.
- Line Perpendicular to a Plane
- Line Parallel to the Plane
The line has no points in common with the plane r⋂α=Ø.
If a line \( r \) is parallel to a plane \( \alpha \), any other plane \( \beta \) that contains \( r \) and is not parallel to \( \alpha \) will intersect \( \alpha \) along a line \( s \), which is parallel to \( r \).
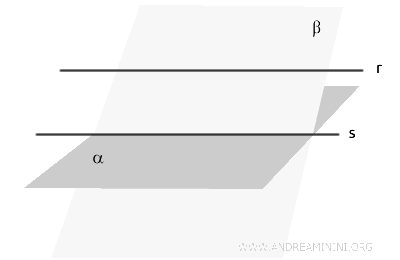
This occurs because lines \( r \) and \( s \), being coplanar, both lie on plane \( \beta \) and never meet.
And so on.
