Distance Between a Line and a Parallel Plane

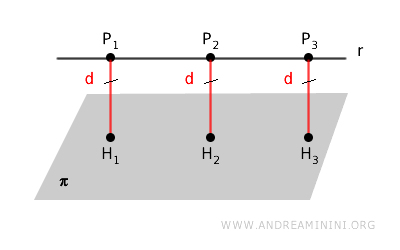
The distance $ d $ between a line $ r $ and a parallel plane $ \pi $ is calculated by selecting a point $ P $ on the line and projecting it perpendicularly onto the plane.
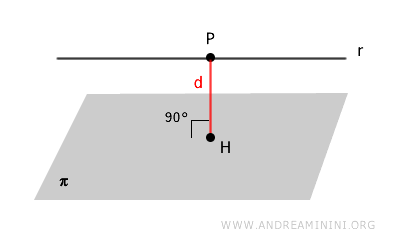
example

The formula to compute the distance $ d $ from a point $ P(x_0, y_0, z_0) $ to a plane defined by the equation $ ax + by + cz + d = 0 $ is:

$$ d = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

This formula gives the length of the perpendicular segment connecting $ P $ to the plane $ \pi $. Since the line $ r $ is parallel to the plane, this distance is the same for any point on the line.

example

Example

Let’s consider the plane $ \pi $ described by the equation:

$$ 2x - 3y + 6z + 9 = 0 $$

Suppose the line $ r $ is defined by the parametric equations:

$$ x = 13 + 3t $$

$$ y = 2t $$

$$ z = 0 $$

To confirm that the line $ r $ is parallel to the plane $ \pi $, we calculate the dot product of the plane’s normal vector $ (2, -3, 6) $ and the line’s direction vector $ (3, 2, 0) $:

$$ 2 \cdot 3 + (-3) \cdot 2 + 6 \cdot 0 = 6 - 6 + 0 = 0 $$

Since the dot product is zero, the line is indeed parallel to the plane.

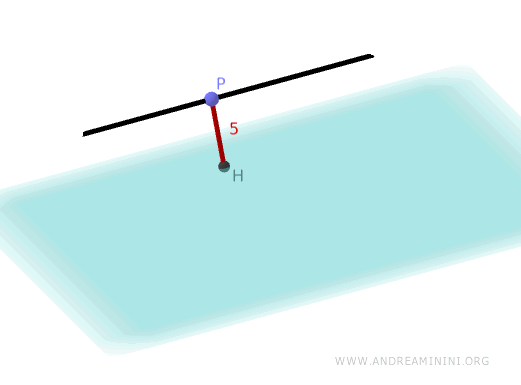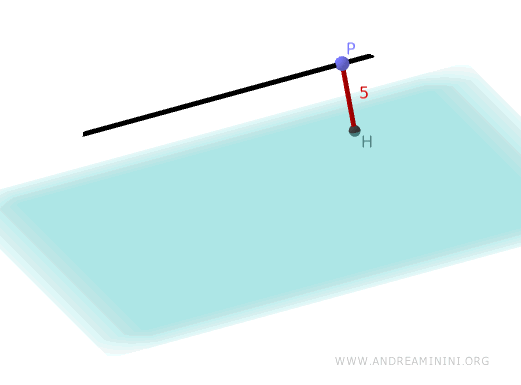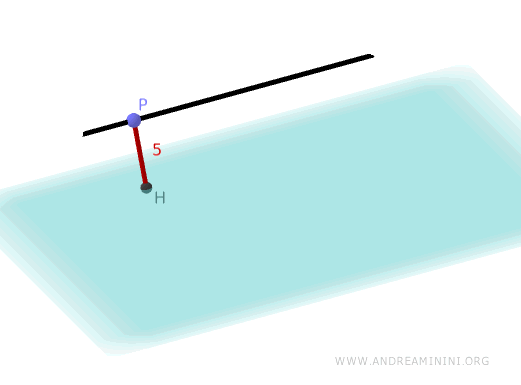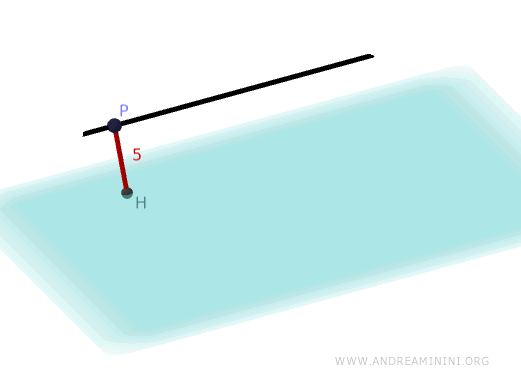
Next, we select a point on the line $ r $. For $ t = 0 $, the point is $ (13, 0, 0) $. Using the distance formula, we calculate:

$$ d = \frac{|2(13) - 3(0) + 6(0) + 9|}{\sqrt{2^2 + (-3)^2 + 6^2}} $$

$$ d = \frac{|26 + 9|}{\sqrt{4 + 9 + 36}} $$

$$ d = \frac{35}{\sqrt{49}} $$

$$ d = \frac{35}{7} = 5 $$

Therefore, the distance between the line $ r $ and the plane $ \pi $ is 5.

distance between a line and a plane

And so on.