Parallel Planes
Two planes in space are considered parallel if they meet one of the following conditions:
- They do not share any points, meaning they never intersect. These are called non-coincident parallel planes.
- They share every point, meaning they are identical. These are referred to as coincident planes.
For example, the floors of two levels in a building, assuming they are perfectly horizontal, form a pair of non-coincident parallel planes.
Distance Between Parallel Planes
The distance between two non-coincident parallel planes is the length of the perpendicular segment connecting a point on one plane to a point on the other.
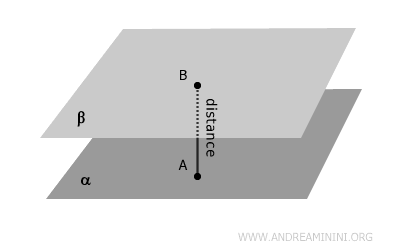
This distance is the same for all points on both planes.
How to Calculate the Distance Between Two Parallel Planes
In analytic geometry, the equations of two parallel planes can be written as:
$$ Ax + By + Cz + D_1 = 0 $$
$$ Ax + By + Cz + D_2 = 0 $$
The distance between these two planes is given by the formula:
$$ d = \frac{|D_2 - D_1|}{\sqrt{A^2 + B^2 + C^2}} $$
where \( A, B, C \) are the coefficients of the normal vector to the planes.
Note: If the distance is zero \( d=0 \), the two planes are coincident. If the distance is a positive value \( d>0 \), the planes are distinct but parallel.
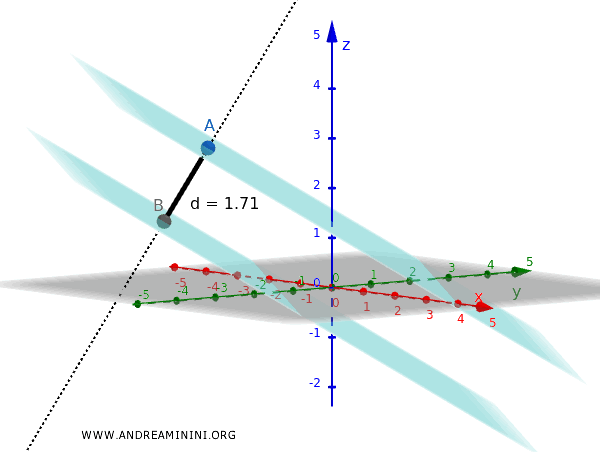
Example
Consider two parallel planes with the following equations:
$$ 2x + 3y + 6z + 4 = 0 $$
$$ 2x + 3y + 6z - 8 = 0 $$
Using the formula:
$$ d = \frac{| -8 - 4 |}{\sqrt{2^2 + 3^2 + 6^2}} = \frac{12}{\sqrt{4+9+36}} = \frac{12}{\sqrt{49}} = \frac{12}{7} \approx 1.71 $$
Thus, the distance between the two planes is approximately 1.71 units.
Properties of Parallel Planes
Parallelism between planes follows these fundamental properties:
- Reflexive property: Every plane is parallel to itself. $$ \alpha \parallel \alpha $$
- Symmetric property: If a plane \(\alpha\) is parallel to a plane \(\beta\), then \(\beta\) is also parallel to \(\alpha\). $$ \alpha \parallel \beta \quad \Rightarrow \quad \beta \parallel \alpha $$
- Transitive property: If a plane \(\alpha\) is parallel to a plane \(\beta\), and \(\beta\) is parallel to a plane \(\gamma\), then \(\alpha\) is also parallel to \(\gamma\). $$ \alpha \parallel \beta, \quad \beta \parallel \gamma \quad \Rightarrow \quad \alpha \parallel \gamma $$
These three properties establish that parallelism between planes is an equivalence relation in geometry.
Condition for Parallel Planes
Given the general equations of two planes: $$ ax+by+cz+d = 0 $$ $$ a'x+b'y+c'z+d' = 0 $$ the planes are parallel if $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$. In particular, they are identical if $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} $$
Let’s examine two planes defined by these general equations:
$$ ax + by + cz + d = 0 $$
$$ a'x + b'y + c'z + d' = 0 $$
The coefficients $ a, b, c $ and $ a', b', c' $ are the components of the normal vectors to the two planes:
$$ \vec{n} = (a, b, c), \quad \vec{n'} = (a', b', c') $$
The planes are parallel if and only if their normal vectors are proportional - that is, if there exists a real number $ k $ such that:
$$ \vec{n} = k \, \vec{n'} \quad \text{or equivalently} \quad (a, b, c) = k \, (a', b', c') $$
In other words, this means:
$$
\begin{cases}
a = k a' \\
b = k b' \\
c = k c'
\end{cases}
$$
Simply put, the ratios of the corresponding coefficients must all be equal:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = k $$
That is, $ a, b, c $ must each be proportional to $ a', b', c' $.
Important. If one or more of $ a', b', c' $ are zero, then for proportionality to hold, the corresponding coefficients $ a, b, c $ must also be zero. In other words:
- If $ a' = 0 $, then $ a = 0 $ must also be true
- If $ b' = 0 $, then $ b = 0 $ must also be true
- If $ c' = 0 $, then $ c = 0 $ must also be true
Condition for Coinciding Planes
Two planes:
$$ a x + b y + c z + d = 0 $$
$$ a' x + b' y + c' z + d' = 0 $$
are identical if there exists a real number $ k \neq 0 $ such that:
$$ (a, b, c, d) = k \cdot (a', b', c', d') $$
In other words, the entire set of coefficients - including the constant term - must be proportional.
In practice, this condition can be verified by checking:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} = k $$
as long as all denominators are non-zero.
Note. If one or more denominators are zero, the corresponding numerators must also be zero, and the remaining coefficients must still satisfy the proportionality condition. For instance, if $ d' = 0 $, then $ d = 0 $ must also hold, and vice versa.
Example
Consider the following planes:
$$ 3x + 6y - 9z + 12 = 0 $$
$$ x + 2y - 3z + 4 = 0 $$
Let’s compute the ratios of the corresponding coefficients:
$$ \frac{3}{1} = 3, \quad \frac{6}{2} = 3, \quad \frac{-9}{-3} = 3 $$
Since all these ratios are equal:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = 3 $$
we can conclude that the normal vectors are proportional - meaning the planes are parallel.
Note. The coefficients correspond to the components of the normal vectors to the planes: $$ \vec{n} = (3, 6, -9), \quad \vec{n'} = (1, 2, -3) $$ A "normal vector" is a vector perpendicular to the plane. Here’s an example of a normal vector:

Next, let’s check the constant terms:
$$ \frac{12}{4} = 3 $$
Again, this ratio is equal to 3. Therefore:
$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} = 3 $$
This shows that the two planes are not only parallel - they are in fact identical.
Additional Notes
Here are a few additional insights on parallel planes:
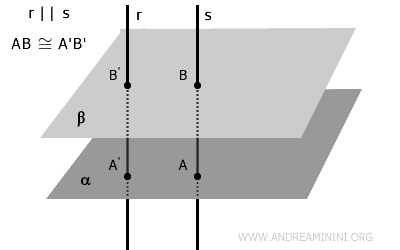
- If two planes are parallel, then any line perpendicular to one of them is also perpendicular to the other.
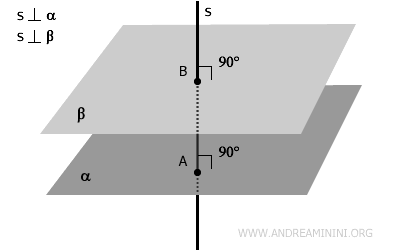
- If two parallel planes are intersected by two parallel lines - whether perpendicularly or at an angle - the segments of these lines between the planes are congruent. $$ AB \cong A'B' $$.
And so on.
