Distance from a Point to a Plane

The distance between a point P and a plane is the length of the perpendicular segment connecting point P to the plane.

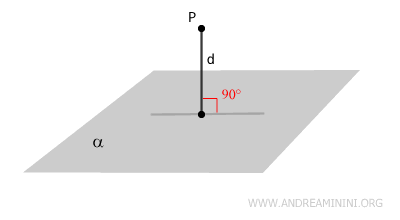
In other words, the distance from a point P to a plane is the length of the perpendicular line segment that extends from point P to the plane.

The distance is always a non-negative value. If the point lies on the plane, the distance is zero.

How to Calculate the Distance Between a Point and a Plane

The shortest distance between a point P and a plane α in space is the length of the perpendicular segment from P to the plane α.

$$ d(P, \alpha ) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$

Example

Consider point P with coordinates (x;y;z) = (1;3;2) in three-dimensional space:

$$ P = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} $$

The Cartesian equation of the plane is:

$$ 4x-2y+z-5 = 0 $$

The distance between the point and the plane is calculated using the formula above.

$$ d(P, \alpha) = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}} $$

The parameters of the plane equation are a=4, b=-2, c=1, and d=-5:

$$ d(P, \alpha) = \frac{|4 \cdot x_0 - 2 \cdot y_0 + 1 \cdot z_0 - 5|}{\sqrt{4^2 + (-2)^2 + 1^2}} $$

$$ d(P, \alpha) = \frac{|4 \cdot x_0 - 2 \cdot y_0 + 1 \cdot z_0 - 5|}{\sqrt{21}} $$

Substituting the coordinates of the point x₀=1, y₀=3, z₀=2:

$$ d(P, \alpha) = \frac{|4 \cdot 1 - 2 \cdot 3 + 1 \cdot 2 - 5|}{\sqrt{21}} $$

$$ d(P, \alpha) = \frac{|-5|}{\sqrt{21}} $$

$$ d(P, \alpha) = \frac{5}{\sqrt{21}} = 1.09 $$

Therefore, the distance between point P and the plane is 1.09.

In the following graphic, this is represented by the red line between point P and the plane.

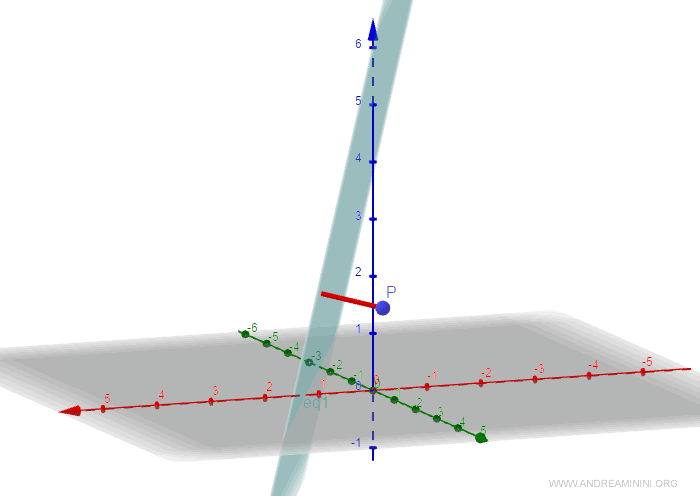
It is the length of the perpendicular segment from point P to the plane.

Notes

Additional notes on the distance between a point and a plane

• Theorem
  Given a plane \( \alpha \) and a point \( P \) not lying on it, the perpendicular segment \( PH \) drawn from \( P \) to the plane is shorter than any oblique segment \( PQ \).
  

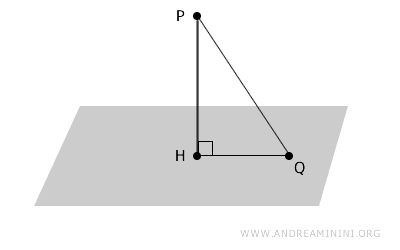
  Proof. Let \( PH \) be the perpendicular segment from \( P \) to the plane \( \alpha \), and let \( PQ \) be any oblique segment where \( Q \) lies on \( \alpha \). The three points form a right triangle \( PHQ \). By the Pythagorean theorem, the oblique side is always longer than either of the legs, so \( PQ > PH \). Therefore, the perpendicular segment \( PH \) represents the shortest distance between \( P \) and the plane.

• Corollary
  If two oblique segments drawn from a point \( P \) to a plane \( \alpha \) have congruent projections on the plane, then the segments themselves are congruent, and the reverse is also true. 
  

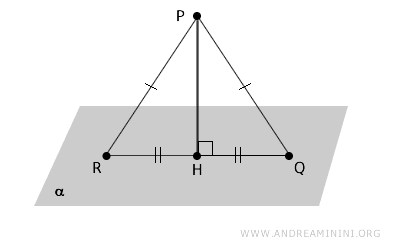
  Proof. Consider two congruent oblique segments \( PQ \cong PR \) and the perpendicular segment \( PH \) drawn from \( P \) to the plane \( \alpha \). By the criteria for triangle congruence, the triangles \( PHR \cong PHQ \) are congruent because they share two equal sides and a congruent angle. Thus, the projections \( HR \cong HQ \) are congruent, meaning congruent oblique segments \( PR \cong PQ \) have congruent projections \( HR \cong HQ \) on the plane \( \alpha \).

• Corollary
  If two oblique segments drawn from a point \( P \) to a plane \( \alpha \) have unequal projections, the segment with the larger projection is longer.
  

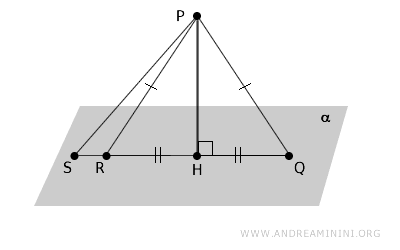
  Example. In this case, the oblique segment \( PS \) is longer than \( PR \). Consequently, its projection \( HS \) is also greater, meaning \( HS > HR \).

And so on.