Angle Between a Line and a Plane

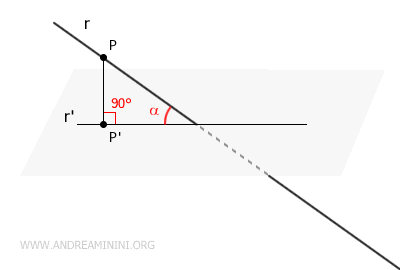
The angle between a line (r) and a plane is defined as the angle α formed between the line itself and its orthogonal projection (r') onto the plane.

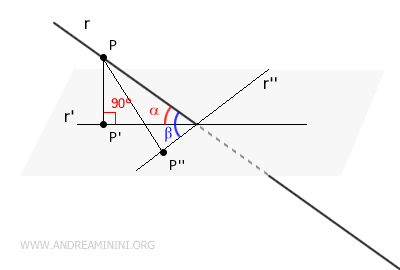
A single line can form various angles with a plane, depending on how its projection is considered.

This happens because there are infinitely many planes that can intersect a line.

However, not all these angles are equally significant.

The angle that is generally considered the angle between the line and the plane is the minimum angle.

This angle occurs when the projection of the line onto the plane is perpendicular (90°) to the plane itself.

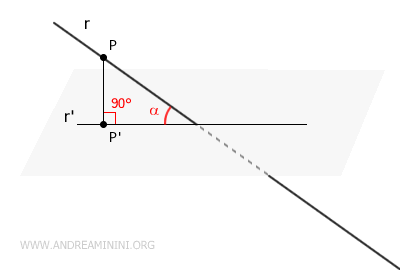
A Practical Example

In this example, imagine a line r and a plane α.

If we consider a plane β (different from plane α) that intersects line r, the projection r' of line r onto plane α forms an angle of 93.5°.

However, if we choose another plane β' passing through line r, the angle between line r and plane α would be different.

For example, the angle between the line and plane α is now 99.71°.

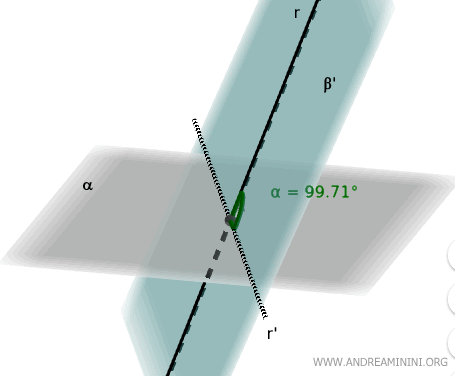
Note: Plane α and line r remain the same. I simply considered a different plane β passing through line r that creates a different projection r' on plane α. For this reason, the angle between line r and its projection r' is different.

To find the minimum angle, we should choose a plane β'' passing through line r that is also a perpendicular plane (90°) to plane α.

In this case, the projection r' of line r onto plane α would form an angle of 64.76°, the smallest possible angle.

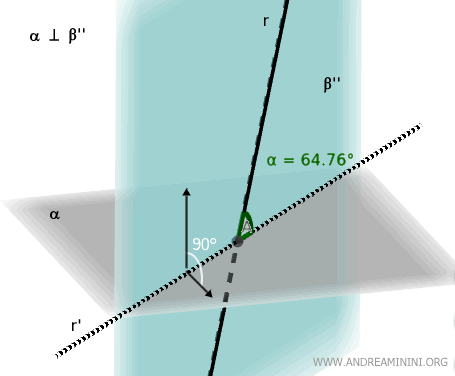
In conclusion, the angle between a line and a plane is defined as the angle between the line and its orthogonal projection onto the plane, and this angle is always the smallest possible angle.

And so on.