Area
In geometry, area measures the extent of a surface on a plane. It can also be described as the amount of space within the perimeter of a shape on a plane.
It is a geometric concept applied to two-dimensional figures, meaning those with two dimensions.
Area is a scalar quantity represented by a non-negative real number that describes the size of a region or shape within a plane.
The standard unit of measurement for area is the square meter (m² or sqm), although multiples and submultiples like square centimeters (cm²) and square kilometers (km²) are also used.
Depending on the context, area can also be measured in other units such as square inches, or hectares (ha), which are used in agriculture and equal 10,000 sqm, among others.
Note. The concept of area has been studied since ancient times. Greek mathematicians like Euclid and Archimedes developed the first systematic theories of area, including methods for calculating the area of various polygons and circles. It is a concept used in numerous fields beyond pure mathematics, such as architecture, civil engineering, agriculture, and geography. It is essential for space planning.
Area in Physics
Area is a derived physical quantity that measures the extent of a flat surface.
It’s termed "derived" because it is based on a fundamental quantity: length (L).
In the International System of Units (SI), the standard unit of area is the square meter (m2). This unit represents the space taken up by a square with sides of 1 meter.
From a dimensional analysis perspective, area is the product of two lengths that define the width and height of a shape.
$$ \text{Area} = [L] \cdot [L] $$
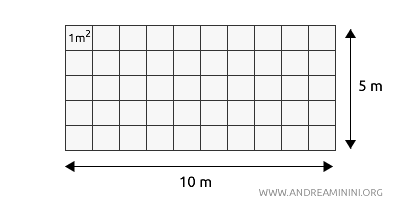
To calculate the area of flat shapes, like a rectangle, you multiply the length of the base by the height.
For example, for a rectangle with a base of 10 meters and a height of 5 meters:
$$ \text{Area} = \text{base} \times \text{height} = (10 \, \text{m}) \times (5 \, \text{m}) = 50 \, \text{m}^2 $$
This calculation not only shows the numerical result ($10 \times 5 = 50$), but also emphasizes the importance of multiplying the units ($m \times m = m^2$).
In essence, the area represents the number of 1-meter squares that fit within the surface of the rectangle.
Calculating Area
The method for calculating area varies depending on the shape:
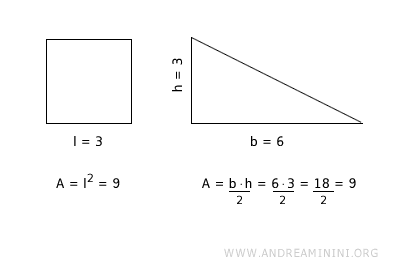
- Triangle Area
The area of a triangle is calculated by dividing the product of the base and height by two. $$ A = \frac{Base \times Height }{2} $$ - Square Area
The area of a square is obtained by squaring one of its sides. $$ A = side \times side = side ^2 $$ - Rectangle and Parallelogram Area
The area of a rectangle or parallelogram is calculated by multiplying the base and height. $$ A = Base \times Height $$ - Rhombus Area
The area of a rhombus is equal to the product of its diagonals d1 and d2 divided by two. $$ A = \frac{d_1 \times d_2 }{2} $$ - Trapezoid Area
The area of a trapezoid is equal to half the product of the height and the sum of the longer base (Base) and the shorter base (base). $$ A = \frac{(Base + base) }{2} \times Height $$ - Circle Area
The area of a circle is calculated by multiplying the square of the circle's radius by the constant pi ( π=3.14... ). $$ A = \pi r^2 $$ - Regular Polygon Area
The area of a regular polygon is calculated by multiplying the perimeter by the apothem and dividing by two. $$ A = \frac{Perimeter \times Apothem }{2} $$ - Irregular Figure Area
The area of an irregular figure requires dividing it into simpler shapes or using integration methods.
Square Meter Multiples and Submultiples
In the metric system, the standard unit for measuring area is the square meter (sqm or m2), which represents a square with sides that are each 1 meter long.
The multiples and submultiples of the square meter include:
| mm2 | square millimeters |
| cm2 | square centimeters |
| dm2 | square decimeters |
| m2 | square meters |
| dam2 | square decameters |
| hm2 | square hectometers |
| km2 | square kilometers |
Each unit is 100 times larger than the one directly below it and one hundredth of the unit directly above it.
For instance, one square meter (m2) is equal to 100 square decimeters (dm2) and 1/100 of a square decameter (dam2).
Converting Area Units
Area can also be expressed in multiples or submultiples of the square meter. For instance:
- Square centimeter ($cm^2$): equivalent to $10^{-4}$ square meters.
- Square millimeter ($mm^2$): equivalent to $10^{-6}$ square meters.
- Square kilometer ($km^2$): equivalent to $10^6$ square meters.
These conversion factors are essential.
For example, to convert from $m^2$ to $cm^2$, you multiply by $10^4$ because $1 \, cm = 10^{-2} \, m$. Therefore:
$$ 1 \, cm^2 = (10^{-2} \, m) \times (10^{-2} \, m) = 10^{-4} \, m^2 $$
The same principle applies for other conversions, such as from square millimeters to square meters:
$$ 1 \, mm^2 = (10^{-3} \, m) \times (10^{-3} \, m) = 10^{-6} \, m^2 $$
And for square kilometers:
$$ 1 \, km^2 = (10^3 \, m) \times (10^3 \, m) = 10^6 \, m^2 $$
In general, when converting area units, it’s important to square the conversion factor.
For example, if I have an area of 100 m² and want to convert it to square decimeters (dm2), I need to multiply by 10 squared, not just 10 as I would for a length. $$ 100 \ m^2 = 100 \cdot 10^2 \ dm^2 = 10000 \ dm^2 $$ If I want to convert it to square centimeters (cm2), I apply the square of 102. $$ 100 \ m^2 = 100 \cdot (10^2)^2 \ cm^2 = 100 \cdot 10^4 \ cm^2 = 10^6 \ cm^2 $$ To convert it to square millimeters (mm2), I use the square of 103. $$ 100 \ m^2 = 100 \cdot (10^3)^2 \ mm^2 = 100 \cdot 10^6 \ mm^2 = 10^8 \ mm^2 $$ And so forth.
Equivalence Classes of Area
Two geometric figures belong to the same equivalence class if they have the same area,
The area of geometric figures forms equivalence classes,
Polygons that have the same area belong to the same equivalence class and are also called equivalent polygons.
And so on.
