Lines of Symmetry

Lines of symmetry are imaginary lines that divide a geometric shape into two mirror-image halves.

The number and presence of these lines vary depending on the shape.

Geometric shapes can have one or more lines of symmetry. Here are some examples of shapes and their lines of symmetry:

• Isosceles Triangle
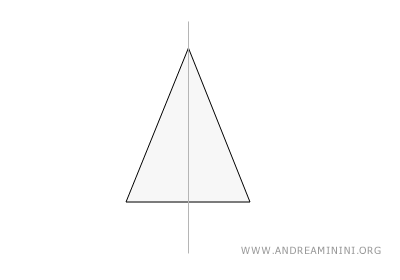
  This triangle has two equal sides and one line of symmetry that runs from the vertex opposite the base, splitting the triangle into two equal halves. Therefore, it has just one line of symmetry.
  
• Equilateral Triangle
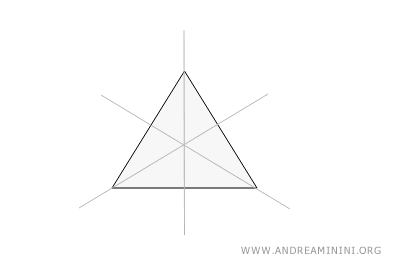
  In this triangle, all sides and angles are equal. It has three lines of symmetry, each passing through a vertex and dividing the triangle into two equal halves.
  
• Scalene Triangle
  This triangle has no equal sides or angles, so it does not have any lines of symmetry.
• Square
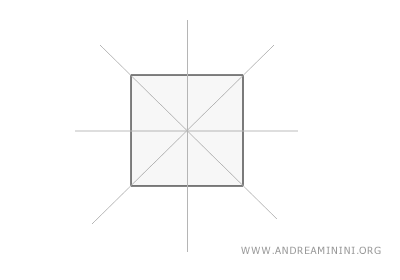
  A square has four equal sides and four right angles. It has four lines of symmetry: two that pass through opposite vertices and two that pass through the midpoints of opposite sides.
  
• Rectangle
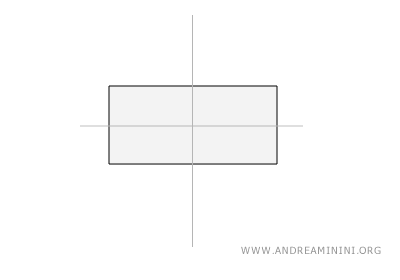
  A rectangle has two lines of symmetry, each passing through the midpoints of opposite sides.
  
• Rhombus
  This shape has four equal sides but not necessarily right angles. It has two lines of symmetry that run through opposite vertices.
  
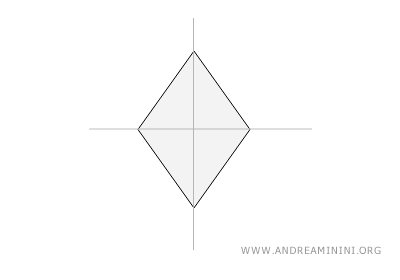
• Kite
  The kite has one line of symmetry that passes through the midpoints of the opposite sides.
  
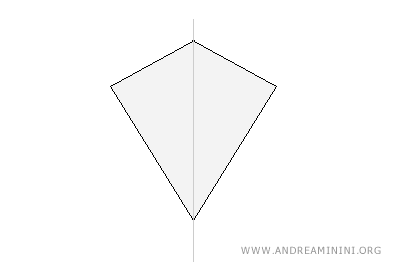
• Regular Pentagon
  This shape has five equal sides and angles, giving it five lines of symmetry. Each line runs through a vertex, dividing the pentagon into two equal halves.
  
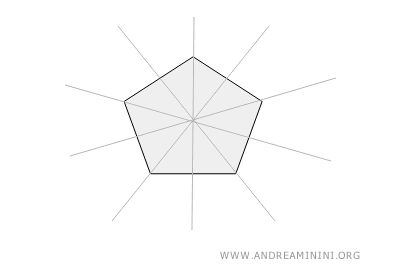
• Regular Hexagon
  With six equal sides and angles, a regular hexagon has six lines of symmetry, each passing through a vertex and dividing the shape into two equal halves.
  
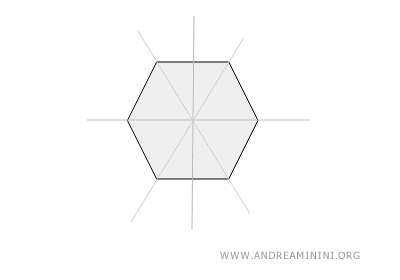
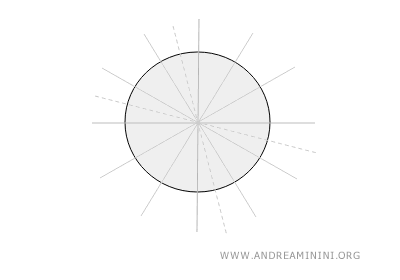
• Circle
  A circle is perfectly symmetrical, with an infinite number of lines of symmetry. Every diameter of the circle acts as a line of symmetry.
  

Notes

Additional points about lines of symmetry:

• A line is considered a line of symmetry for a shape if the reflection symmetry across that line creates a invarant figure.

  Here, a "unified shape" means a shape that matches its transformed image after a geometric transformation, in this case, reflection symmetry.

And so on.