Axial Symmetry

Axial symmetry (also known as reflection) is an isometric transformation where every point of a figure is reflected across a line, called the axis of symmetry, such that it appears at the same distance on the opposite side.

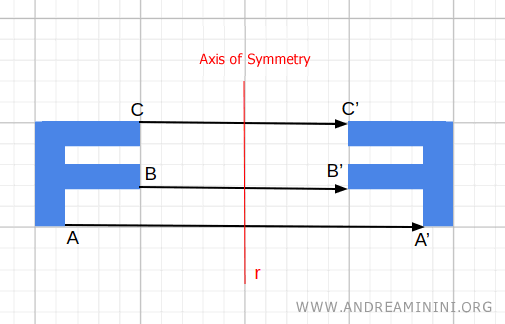
In essence, axial symmetry divides the plane into two parts using a line r, referred to as the axis of symmetry.

For each point A on one side of the line, there is a corresponding point A' on the other side.

The line that connects these two points, AA', is always perpendicular to line r, and its midpoint lies directly on the axis of symmetry.

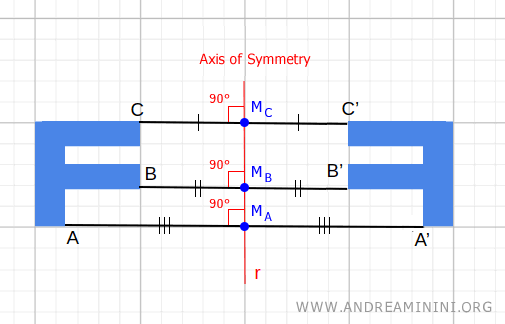
This is why it's termed "axial" - the line r serves as the axis for the segment that links the two points AA'.

• r is perpendicular to the segment AA'
• r passes through the midpoint of the segment AA'

Note: Axial symmetry is an isometry because the figure is reflected from one half-plane to the other without altering its shape, size, or the distance between points. The two figures in the half-planes are congruent to each other.

A Practical Example

For example, a figure on the left half-plane is reflected onto the right half-plane, perpendicular to and equidistant from the axis of symmetry r.

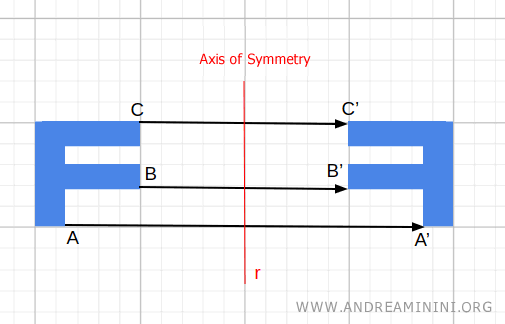
Point C is reflected to point C' in the right half-plane.

Both point C and point C' are 5 units away from the axis of symmetry.

The segment CC' connecting these two points has its midpoint on the axis of symmetry r.

The Formal Definition of Axial Symmetry

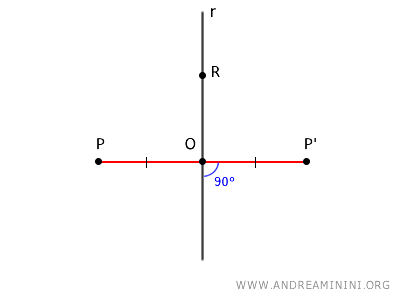
The line r is known as the axis of symmetry.

Thus, the segments OP and OP' are congruent.

$$ \overline{OP} \cong \overline{OP'} $$

All points R on line r remain unchanged by the transformation, as their position does not change after the reflection.

In other words, all points R on the axis of symmetry are fixed points of the transformation.

Types of Axial Symmetry

There are two main types of axial symmetry:

• Reflection
  This is axial symmetry that occurs within a plane, meaning it’s a transformation in two-dimensional space.
• Flipping
  This is axial symmetry in three-dimensional space.

Notable Axial Symmetries in Analytic Geometry

Some axial symmetries are considered "notable" because they involve the Cartesian axes of the plane, the bisectors, or lines parallel to the axes of the plane.

• Symmetry with respect to the x-axis
  In this case, the axis of symmetry is the x-axis. To calculate the coordinates of the corresponding point P'(x';y') of a point P(x;y), use the following equations: $$ \begin{cases} x' = x \\ \\ y' = -y \end{cases} $$  Two points symmetric with respect to the x-axis will have opposite y-coordinates and the same x-coordinate.

  Example: The x-component of the Cartesian coordinates remains constant, while the y-component y'=-y is inverted.
  

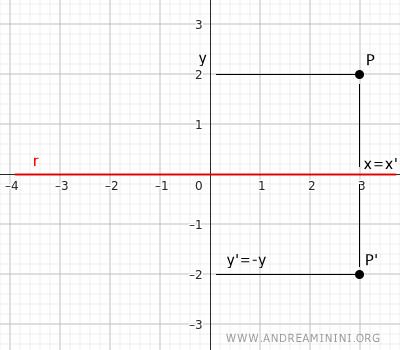
• Symmetry with respect to the y-axis
  The axis of symmetry is the y-axis of the Cartesian plane. To find the coordinates of the corresponding point P'(x';y') of a point P(x;y), use these equations: $$ \begin{cases} x' = -x \\ \\ y' = y \end{cases} $$ Two points symmetric with respect to the y-axis have opposite x-coordinates and the same y-coordinate.

  Example: In this case, the y-component of the Cartesian coordinates stays the same while the x-component is inverted.
  

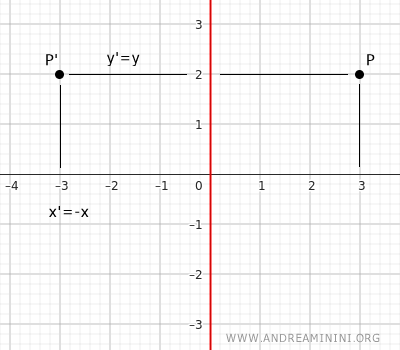
• Symmetry with respect to a line parallel to the x-axis
  Consider a line y=k parallel to the x-axis as the axis of symmetry. The equations for the isometric transformation are: $$ \begin{cases} x' = x \\ \\ y' = 2k-y \end{cases} $$

  Proof: In this case, the x-coordinate x'=x remains the same, while the y-component y' is different. The midpoint y_M of segment PP with respect to the y-coordinates is the average of y and y': $$ k = \frac{y+y'}{2} $$ From this, we derive the y-coordinate y': $$ y' = 2k - y $$ Here's a practical example.
  

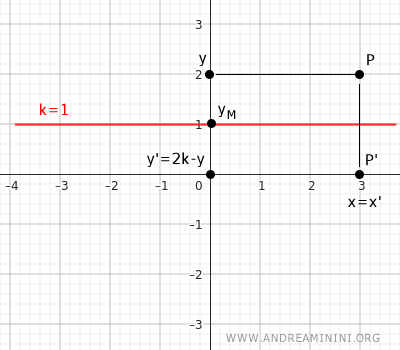
• Symmetry with respect to a line parallel to the y-axis
  In this case, the axis of symmetry is a line x=k parallel to the y-axis. The equations for the isometric transformation are: $$ \begin{cases} x' = 2k-x \\ \\ y' = y \end{cases} $$

  Proof: Here, the y-coordinate y' remains unchanged, while the x-component differs. The midpoint M of segment PP is the average of the two points: $$ k = \frac{x+x'}{2} $$ From this, we derive the equation for the x-coordinate x': $$ x' = 2k - x $$ Here's a practical example.
  

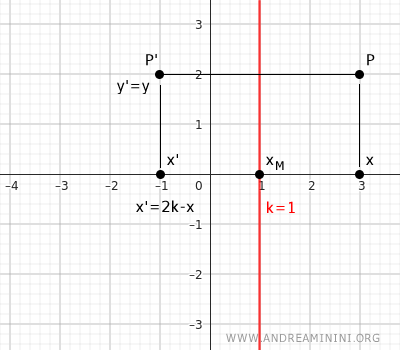
• Symmetry with respect to the quadrant bisector
  The axis of symmetry is the bisector of the quadrants. If the bisector lies in the first and third quadrants of the Cartesian plane, the equations of the axial transformation are: $$ \begin{cases} x' = y \\ \\ y' = x \end{cases} $$ Conversely, if the bisector is in the second and fourth quadrants, the transformation equations are: $$ \begin{cases} x' = -y \\ \\ y' = -x \end{cases} $$

  Example: Here is an example of axial symmetry with respect to the bisector of the first quadrant. The coordinate components swap places, so x'=y and y'=x.
  
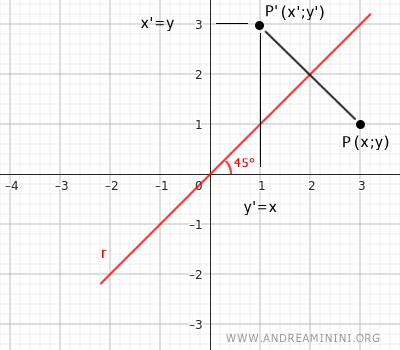
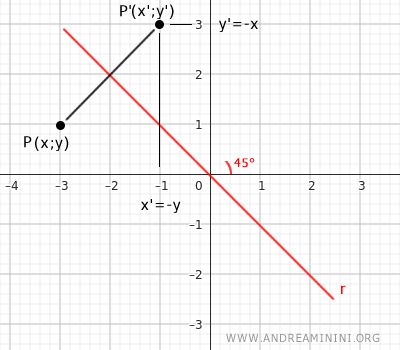
  This next example illustrates axial symmetry with respect to the bisector of the second quadrant. Each coordinate component becomes the opposite of the other, that is, x'=-y and y'=-x.
  

• Reflection across a line (y = mx + q)
  To determine the reflection $P'(x', y')$ of a point $P(x, y)$ across a line $r$ given by the equation $ y = mx + q $, two fundamental conditions must hold:
  • Perpendicularity
    The segment $PP'$ must be perpendicular to the line $r$. Consequently, the slope of $PP'$ is the negative reciprocal of $m$: $$ \frac{y' - y}{x' - x} = -\frac{1}{m} $$
  • Equidistance
    The midpoint of $PP'$ must lie on the line $r$. In other words, the point $$ M\!\left(\frac{x+x'}{2}, \; \frac{y+y'}{2}\right) $$ belongs to $r$, which leads to the condition: $$ \frac{y+y'}{2} = m \cdot \frac{x+x'}{2} + q $$
  Solving this system for $x'$ and $y'$ gives the coordinates of the reflected point: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$

  Example. Suppose we want the reflection of $P(2,3)$ across the line $ r: \; y = 2x + 1 $. Using the transformation formulas: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$ Substituting $m=2, q=1, x=2, y=3$: $$ \begin{cases} x' = \frac{(1-4)\cdot 2 + 2\cdot 2\cdot 3 - 2\cdot 2\cdot 1}{2^2+1} \\ \\ y' = \frac{(4-1)\cdot 3 + 2\cdot 2\cdot 2 + 2\cdot 1}{5} \end{cases} $$ $$ \begin{cases}
  x' = \frac{-6 + 12 - 4}{5} = \frac{2}{5} = 0.4 \\ \\ y' = \frac{9 + 8 + 2}{5} = \frac{19}{5} = 3.8 \end{cases} $$ Thus, the reflection of $ P $ across line $ r $ is $ P'(0.4,\;3.8) $.
  

• Symmetry with respect to the line (y = mx)
  If the axis of symmetry is the line $ y = m x $ through the origin, the coordinates of the reflected point $(x',y')$ of a given point $(x,y)$ can be obtained from the following relations: $$ \begin{cases} x' = x \cos 2\alpha + y \sin 2\alpha \\[6pt] y' = x \sin 2\alpha - y \cos 2\alpha \end{cases} $$ where $\alpha = \arctan(m)$ is the angle that the line $y=mx$ makes with the $x$-axis.

  Example. Find the reflection of the point $(2,1)$ across the line $y=x$. Here, the line $y=x$ has slope $m=1$, so $\alpha = \arctan(1) = \tfrac{\pi}{4}$. Doubling the angle gives: $$ \cos 2\alpha = \cos \tfrac{\pi}{2} = 0, \qquad \sin 2\alpha = \sin \tfrac{\pi}{2} = 1 $$ Substituting into the formula: $$ \begin{cases} x' = 2 \cdot 0 + 1 \cdot 1 = 1 \\[6pt] y' = 2 \cdot 1 - 1 \cdot 0 = 2 \end{cases} $$ Thus, the reflection of $(2,1)$ across the line $y=x$ is $(x',y') = (1,2)$.
  
  Proof. Start with the general formula for reflection across the line $ y=mx+q $: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$ If the line passes through the origin ($q=0$), this reduces to: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx}{m^2+1} \end{cases} $$ Since $ m = \tan \alpha $, substitution yields: $$ \begin{cases} x' = \frac{(1-\tan^2 \alpha)x + 2 \tan \alpha \, y}{1+\tan^2 \alpha} \\ \\ y' = \frac{(\tan^2 \alpha -1)y + 2 \tan \alpha \, x}{1+\tan^2 \alpha} \end{cases} $$ Simplifying gives: $$ \begin{cases} x'= \frac{1-\tan^2 \alpha }{1+\tan^2 \alpha }\,x + \frac{2 \tan \alpha}{1+\tan^2 \alpha }\,y \\ \\ y'= \frac{2 \tan \alpha}{1+\tan^2 \alpha}\,x - \frac{1-\tan^2 \alpha}{1+\tan^2 \alpha}\,y \end{cases} $$ Finally, applying the trigonometric identities $ \cos 2 \alpha = \tfrac{1- \tan^2 \alpha}{1 + \tan^2 \alpha} $ and $ \sin 2 \alpha = \tfrac{2 \tan \alpha}{1 + \tan^2 \alpha} $, we obtain: $$ \begin{cases} x'= x \cos 2 \alpha + y \sin 2 \alpha \\ \\ y'= x \sin 2 \alpha - y \cos 2 \alpha \end{cases} $$ which completes the proof.

These are the most common cases of axial symmetry.

It’s also possible to calculate reflection with respect to a line at any angle. In such cases, however, you need to use the reflection matrix. I'll discuss this in the next section.

Reflection Matrix

In the plane, reflection with respect to a line y=mx (the axis of symmetry) passing through the origin of the Cartesian plane can be obtained using the reflection matrix.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = A \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$

Where (x;y) are the initial coordinates of a point P, and (x';y') are the coordinates of the corresponding point P' after the reflection.

The reflection matrix is:

$$ A = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} $$

The term α is the angle that the line y=mx forms with the positive x-axis.

Note: The angle α can be determined using the arctangent of the slope (m) of the line y=mx, knowing that m=y/x. $$ \alpha = \arctan(m) $$ However, note that the formula α=arctan(m) does not work when the line r is perfectly perpendicular to the x-axis (90° or 270°), because in such cases, the slope tends toward infinity.

To better understand its use, let’s go through a practical example.

Example

Consider the point with coordinates x=2 and y=3:

$$ P = (2;3) $$

We plot the point on the Cartesian plane:

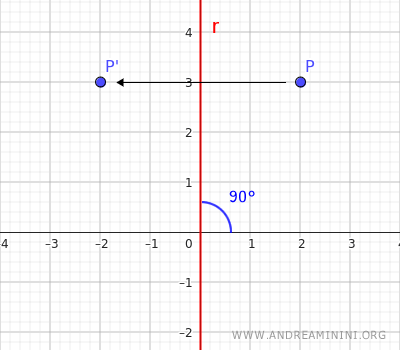
For simplicity, let’s use a line y=mx that forms a 90° (π/2 radians) angle with the positive x-axis.

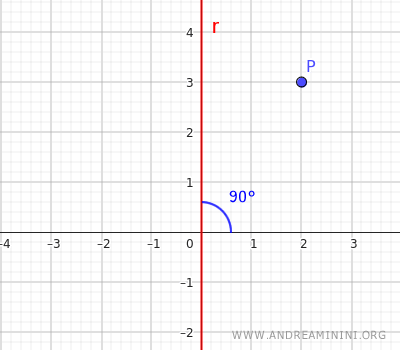
We calculate the new coordinates using the reflection matrix:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$

The initial coordinates of the point are P=(2;3), meaning x=2 and y=3.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

In this example, the angle α=90° is ninety degrees (π/2 radians).

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \cdot 90°) & \sin ( 2 \cdot 90° ) \\ \sin ( 2 \cdot 90°) & - \cos(2 \cdot 90°) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (180°) & \sin ( 180° ) \\ \sin (180°) & - \cos(180°) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Knowing that the sine of 180° is 0, while the cosine of 180° is -1:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & - (-1) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 \cdot 2 + 0 \cdot 3 \\ 0 \cdot 2 + 1 \cdot 3 \end{pmatrix} $$

The final result gives us the coordinates of the reflected point:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} $$

The new coordinates of point P'=(-2;3) after the reflection are x=-2 and y=3.

Axial Symmetry in Space with Solids

Axial symmetry in space is a geometric transformation that reflects a solid across a given axis.

This transformation is an isometry, meaning it preserves the solid's dimensions and shape.

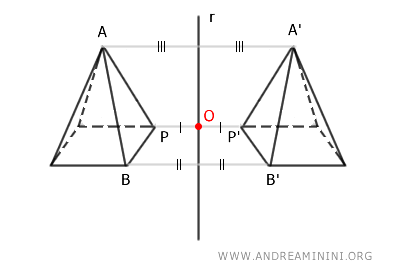
Given a line \( r \) in three-dimensional space, axial symmetry with respect to \( r \) works as follows:

1. All points on the line \( r \) remain unchanged (fixed points).
2. Every other point \( P \) is mapped to a point \( P' \) such that:
   • The segment \( PP' \) is perpendicular to the axis \( r \).
   • Points \( P \) and \( P' \) are equidistant from \( r \). In other words, the segments \( OP \cong OP' \) are congruent, where \( O \) is the intersection of segment \( PP' \) with line \( r \).

What are the properties of axial symmetry in space?

Axial symmetry preserves the distance between points. So, if two points are \( d \) units apart before the transformation, they remain \( d \) units apart afterward.

It also maintains the volume and shape of the solid while keeping the internal angles between its faces unchanged.

In short, a solid reflected through axial symmetry is congruent to the original.

Symmetry with Respect to a Plane

Symmetry with respect to a plane is the three-dimensional counterpart of axial symmetry. While axial symmetry is based on a line, planar symmetry is based on a plane.

In this type of symmetry, a point and its symmetric counterpart are equidistant from the plane and lie along a line that is perpendicular to it.

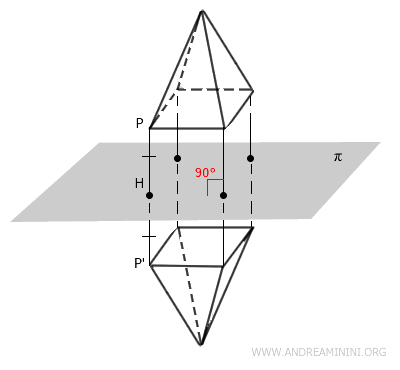
Given a solid figure in three-dimensional space and a symmetry plane \( \pi \):

1. Any point that lies on \( \pi \) remains unchanged (it is a fixed point).
2. Any point \( P \) not on \( \pi \) is mapped to a symmetric point \( P' \) such that:
   - The line \( PP' \) is perpendicular to the plane \( \pi \).
   - The segments \( PH \) and \( P'H \), where \( H \) is the orthogonal projection of \( P \) onto \( \pi \), are equal in length ( \( PH \cong P'H \) ).

Thus, the plane \( \pi \) serves as the plane of symmetry.

Note: In this geometric transformation, figures reflected through plane symmetry are mirror images of each other while remaining congruent in size and shape. The transformation preserves distances, angles, and proportions. Moreover, applying plane symmetry twice with respect to the same plane restores the original figure.

Observations

Here are some additional notes on axial symmetry:

• Axial symmetry is an isometry (proof)
  Consider two points $A$ and $B$ in the plane, and reflect them across a line $r$ to obtain their images $A'$ and $B'$. By definition, $A'$ and $B'$ lie at the same distance from $r$; furthermore, the lines $AA'$ and $BB'$ are perpendicular to $r$, and their intersections $M_A$ and $M_B$ with $r$ are the midpoints of $AA'$ and $BB'$, respectively.
  
  Since $AA'$ and $BB'$ are both perpendicular to $r$, they must be parallel: $ AA' \parallel BB' $. Hence, the distance between them is constant everywhere. Let $C$ be the orthogonal projection of $A$ onto $BB'$, and $C'$ the projection of $A'$. Because $AA'$ and $BB'$ are parallel, the projections $AC$ and $A'C'$ are perpendicular to $BB'$, making them parallel and congruent: $AC \cong A'C'$.
  
  It follows that $AM_A$ and $CM_B$ are congruent, since both measure the distance of symmetric points from $r$, and reflection preserves such distances. Similarly, $A'M_A$ and $C'M_B$ are congruent. From this we deduce that $BC$ and $B'C'$ are congruent as well, $ BC \cong B'C' $, because they arise as differences of congruent segments ( $ BC = BM_B - CM_B $ and $ B'C' = B'M_B - C'M_B $ ). Finally, this implies that $ AB \cong A'B' $, since the right triangles $ ABC $ and $ A'B'C' $ are congruent $ ABC \cong A'B'C' $. They share congruent legs ( $ BC \cong B'C' $ and $ AC \cong A'C' $ ), so their hypotenuses must also be congruent $ AB \cong A'B' $. Thus, axial symmetry preserves the distance between points.
  
• The composition of two axial symmetries with the same axis is equivalent to an identity
  If you perform two axial symmetries S₁ and S₂ (or any even number) with the same axis of symmetry r on a figure, the result is the original figure, meaning it’s an identity because the points remain in the same position. Therefore, a double axial symmetry with the same axis of symmetry is an involutory transformation.
  
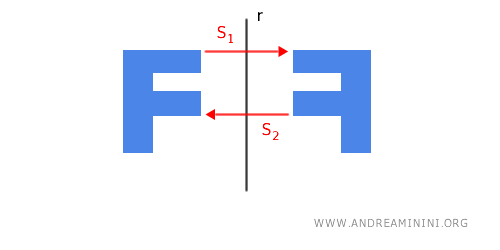
• The composition of two axial symmetries with parallel axes is equivalent to a translation
  If you perform two axial symmetries S₁ and S₂ with two parallel axes of symmetry r₁ and r₂ on a figure, the final result is equivalent to a translation of the original figure.
  

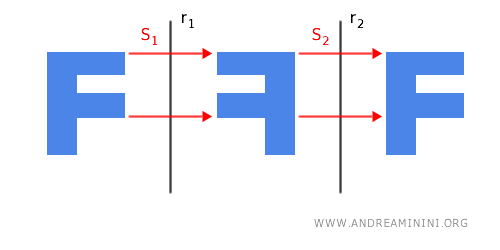
  Note. The translation vector $\vec{v}$ has magnitude equal to twice the distance ($d$) between the two symmetry axes $r_1$ and $r_2$, and it is perpendicular to both: $$ | \vec{v} | = 2d $$ This follows directly from the figure.
  
  Adding the individual displacements gives: $$ | \vec{v} | = 2d_1 + 2d_2 = 2(d_1 + d_2) $$ Since $d_1 + d_2 = d$, the distance between the two axes of symmetry, we finally obtain: $$ | \vec{v} | = 2(d_1 + d_2) = 2d $$

• The composition of two axial symmetries with non-parallel axes is equivalent to a rotation
  If you perform two axial symmetries S₁ and S₂ with two non-parallel axes of symmetry r ₁ and r₂ on a figure, the final result is equivalent to a rotation of the original figure, with the center at the intersection point O of the two symmetry axes r₁ and r₂, and a rotation angle equal to 2α+2β, which is twice the angle γ formed by the symmetry axes.
  
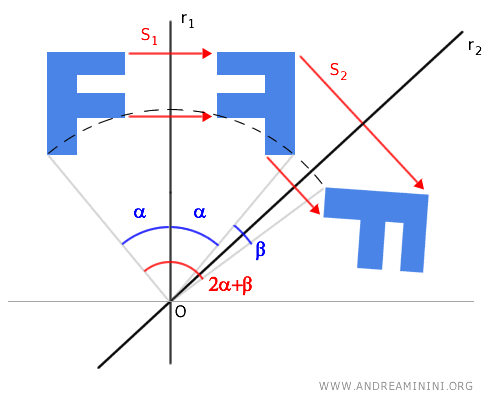
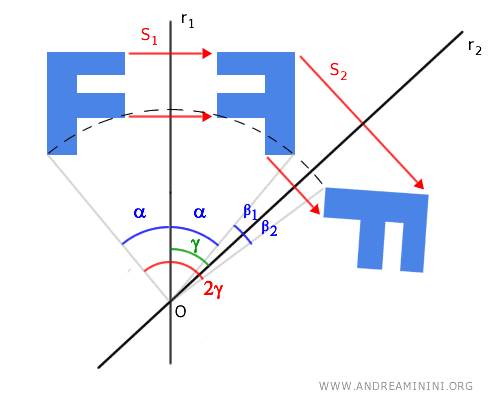
  Since the symmetry axis r₂ is the bisector of the angle 2β=β₁+β₂ with β₁≅β₂, we deduce that α+β₁≅α+β₂ are congruent angles. We call the angle γ≅α+β₁≅α+β₂. This angle γ is also congruent to the angle formed by the symmetry axes r₁ and r₂. Therefore, we can derive the rotation angle more easily as twice the angle γ formed by the symmetry axes r₁ and r₂.
  

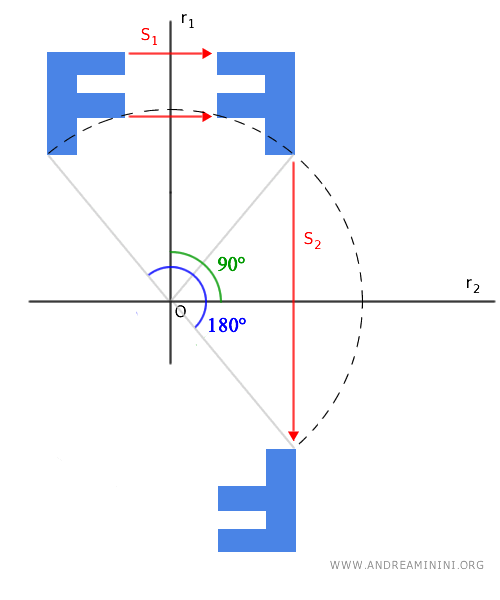
  Note: When the symmetry axes r₁ and r₂ are perpendicular, forming a right angle (90°), the composition of two axial symmetries is equivalent to a 180° rotation (half-turn).
  

• Every isometry can be expressed as a composition of axial symmetries
  This statement is based on some fundamental properties previously demonstrated. In particular, remember that:
  • Rotations, identities, and translations can be represented as compositions of two specific axial symmetries. 
  • Central symmetries are equivalent to a 180-degree (half-turn) rotation around the same center P.
    
    Since every rotation can be decomposed into axial symmetries, central symmetries can also be obtained through a composition of axial symmetries.
  Consequently, every isometry can be realized through a suitable combination of axial symmetries.
• Invariant figures in axial symmetry
  In axial symmetry, the axis of symmetry (r) is an invariant figure because it remains unchanged. More precisely, it is pointwise invariant, since every point on the axis keeps the same coordinates.
  
  Any line perpendicular to the axis of symmetry is also invariant. In this case, however, we describe it as globally invariant: the line itself stays the same, but its individual points are mapped to different coordinates by the transformation.
  

  Note. The line $ r' $ remains unchanged after the transformation, even though its points are relocated. For example, point A is mapped to A'.

• Glide Reflection
  A glide reflection is the composition of a reflection and a translation, where the translation vector runs parallel to the axis of reflection.
  

And so forth.