Involutory Transformations in Geometry

An involutory transformation in geometry (or involution) is a transformation that, when applied twice, returns the object to its original state, essentially acting as an identity transformation.

In simpler terms, it's a transformation \( T \) that, when applied consecutively to a geometric object (e.g., a plane figure, solid, etc.), brings the object back to its starting position.

Mathematically, an involutory transformation can be described as a function that, when applied to any point \( x \), returns the point itself.

$$  T(T(x)) = x  $$

Involutory transformations are found in various branches of geometry, such as Euclidean geometry, projective geometry, and algebraic geometry, and they possess several intriguing properties.

Here are some common examples of involutory geometric transformations:

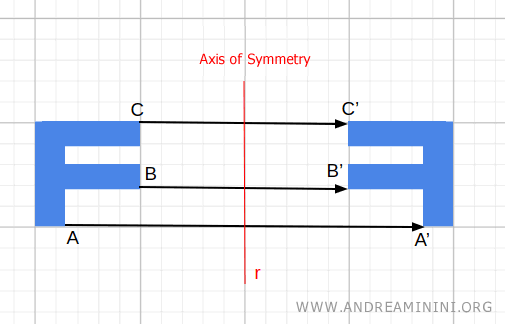
• Reflection (Axial Symmetry)
  Reflecting an object across a line (in the plane) or a plane (in space) is a classic example of an involutory transformation. If you reflect the object twice across the same line or plane, every point returns to its original position.
  
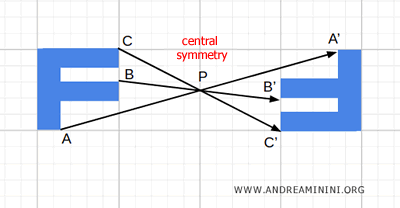
• Central Symmetry
  Central symmetry around a point is another example of an involutory transformation. When you apply the same central symmetry to a point twice, it returns to its original position.
  

And so on.