Dilation and Contraction as Geometric Transformations

Dilation is a geometric transformation that maps each point P(x;y) to a new point P'(x';y') with the following coordinates: $$ \begin{cases} x' = m \cdot x \\ \\ y' = n \cdot y \end{cases} $$ where $ m,n \in \mathbb{R}^+ $ are two positive real numbers.

When m and n are greater than 1, the figure is dilated.

On the other hand, if m and n are between 0 and 1, the figure is contracted.

Thus, contraction is the inverse transformation of dilation.

If n=1, you have a horizontal dilation or contraction depending on whether m>1 or 0<m<1.

If m=1, you have a vertical dilation or contraction depending on whether n>1 or 0<n<1.

For a function $ y = f(x) $, dilation can also be expressed as: $$ y = n \cdot f\left( \frac{x}{m} \right) $$

A Practical Example

Let’s consider four points on the Cartesian plane with coordinates A(2;2), B(4;2), C(4;4), D(2;4), forming the vertices of a square.

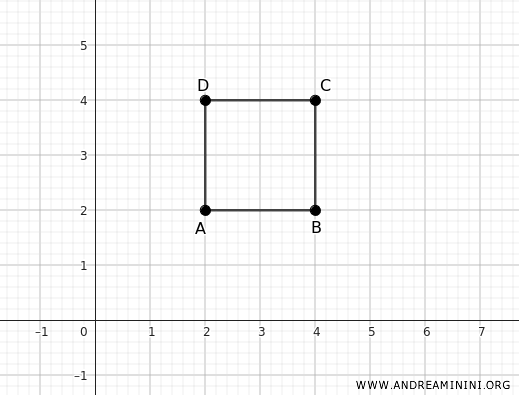
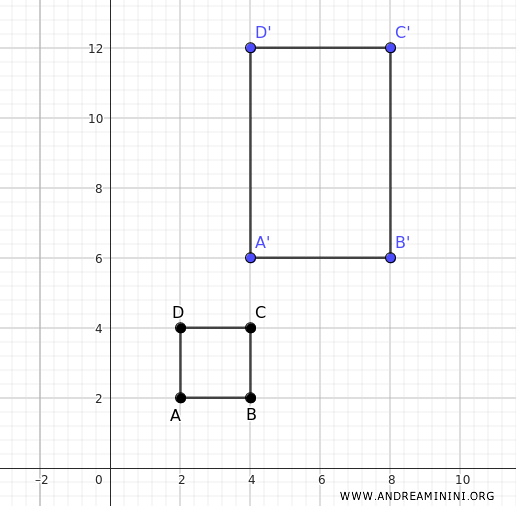
Now, apply a vertical dilation with n=2 and a horizontal dilation with m=3.

The point $ A(2;2) $ becomes $ A'(4;6) $

$$ A' (2 \cdot n ; 2 \cdot m ) = A' (2 \cdot 2 ; 2 \cdot 3 ) = A' (4; 6 ) $$

The point $ B(4;2) $ becomes $ B'(8;6) $

$$ B' (4 \cdot n ; 2 \cdot m ) = B' (4 \cdot 2 ; 2 \cdot 3 ) = B' (8; 6 ) $$

The point $ C(4;4) $ becomes $ C'(8;12) $

$$ C' (4 \cdot n ; 4 \cdot m ) = C' (4 \cdot 2 ; 4 \cdot 3 ) = C' (8; 12 ) $$

The point $ D(2;4) $ becomes $ D'(4;12) $

$$ D' (2 \cdot n ; 4 \cdot m ) = D' (2 \cdot 2 ; 4 \cdot 3 ) = D' (4; 12 ) $$

After the transformation, the new points A', B', C', and D' form a rectangle.

Example 2

To better understand the concept of dilation applied to a function, let’s look at the quadratic function \( f(x) = x^2 \).

$$ f(x) = x^2 $$

The initial graph of the function looks like this:

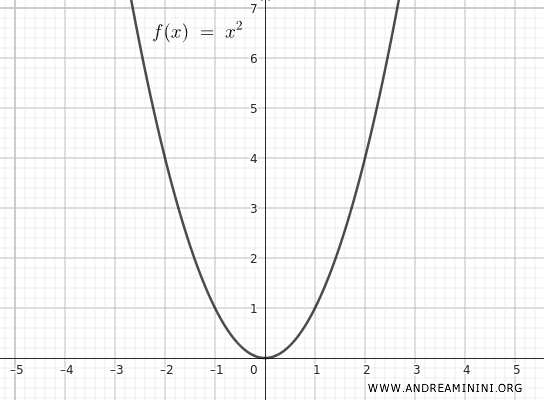
Now, let's explore the possible vertical and horizontal dilations and contractions of the function.

Vertical Dilation/Contraction

To achieve vertical dilation or contraction, multiply the entire function by a factor \( n \).

If \( n > 1 \), the function stretches vertically; if \( 0 < n < 1 \), the function compresses vertically.

$$ y = n \cdot f(x) = n \cdot x^2 $$

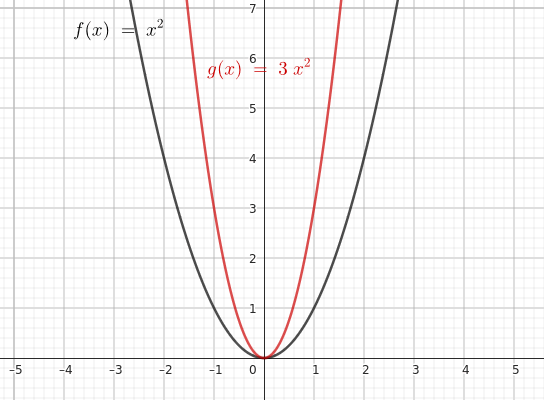
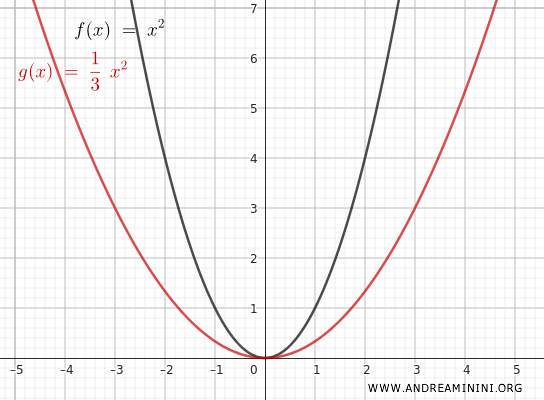
For example, if $ n = 3 $, the function becomes:

$$ y = 3x^2 $$

This transformation triples the value of \( f(x) \) at every point.

If $ n = \frac{1}{3} $ is applied, the function becomes:

$$ y = \frac{1}{3} \cdot x^2 $$

In this case, the function compresses vertically.

Horizontal Dilation/Contraction

For horizontal dilation or contraction, replace \( x \) with \( \frac{x}{m} \) in the function.

If \( m > 1 \), the function stretches horizontally; if \( 0 < m < 1 \), the function compresses horizontally.

$$ y = f\left(\frac{x}{m}\right) = \left(\frac{x}{m}\right)^2 $$

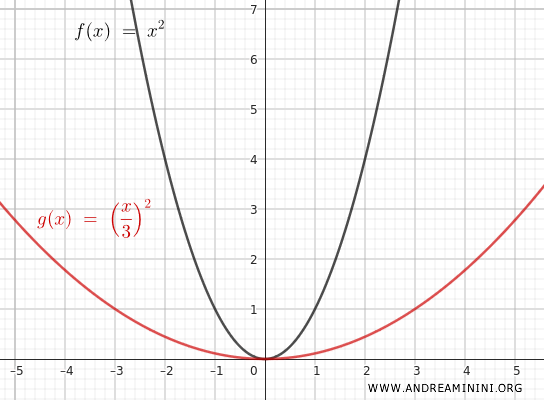
For instance, if \( m = 3 \), the function becomes:

$$ y = \left(\frac{x}{3}\right)^2 = \frac{x^2}{9} $$

This transformation widens the parabola along the x-axis.

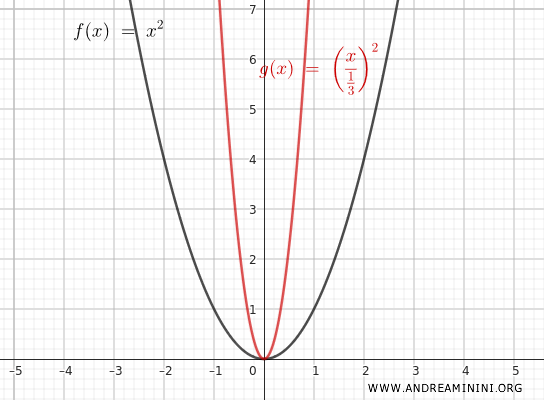
If $ m = \frac{1}{3} $ is applied, the function becomes:

$$ y = \left(\frac{x}{ \frac{1}{3} }\right)^2 = \frac{x^2}{\frac{1}{9}} = 9x^2 $$

In this case, the function compresses horizontally.

Combined Dilation or Contraction

You can also combine both vertical and horizontal dilation or contraction.

In this case, the function becomes:

$$ y = n \cdot f\left(\frac{x}{m}\right) = n \cdot \left(\frac{x}{m}\right)^2 $$

For example, with \( n = 3 \) and \( m = 2 \), the transformed function is:

$$ y = 3 \cdot \left(\frac{x}{2}\right)^2 = 3 \cdot \frac{x^2}{4} = \frac{3x^2}{4} $$

This transformation vertically stretches the function by a factor of 3 and horizontally stretches it by a factor of 2.

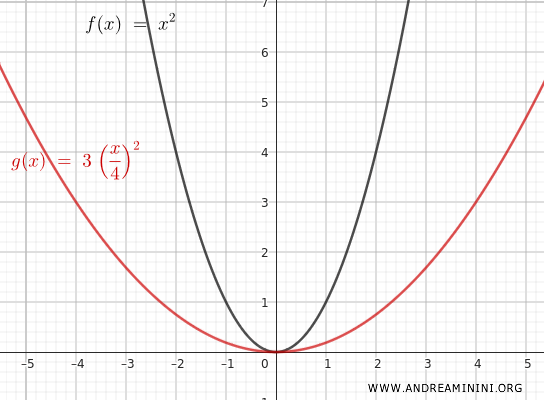
For example, for \( x = 2 \), \( f(x) = 2^2 = 4 \) becomes \( y = \frac{3 \cdot 4}{4} = 3 \). For \( x = 4 \), \( f(x) = 4^2 = 16 \) becomes \( y = \frac{3 \cdot 16}{4} = 12 \).

In conclusion, with the quadratic function \( f(x) = x^2 \), vertical and horizontal dilation affects the size and shape of the parabola.

And so on.