Projective Transformations

Projective transformations are topological changes created by projecting all the points of a figure in space from a projection center, P.

In simpler terms, a projective transformation can be thought of as the shadow cast by an object.

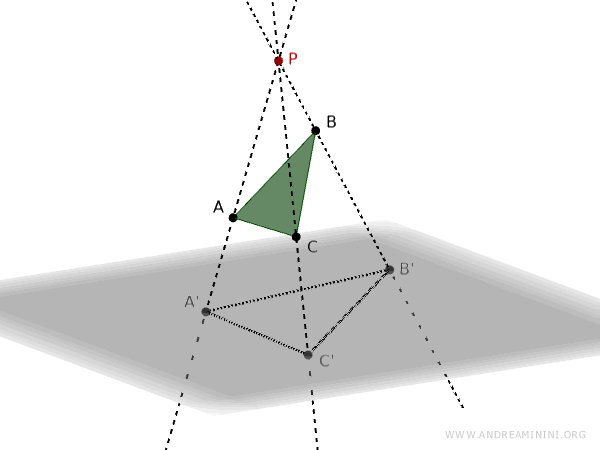
For example, let’s consider a projection point P, a triangle ABC, and a projection plane.

We draw a line through points P and A, known as the projection ray, and identify the intersection point A' on the projection plane.

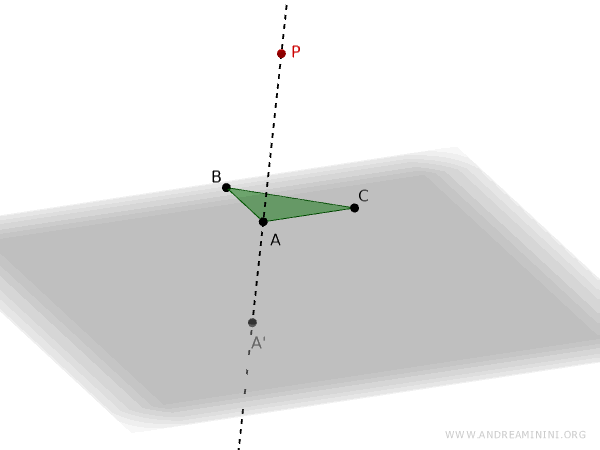
We then repeat the same process for point B.

Drawing a line through points P and B, we find the intersection point B' on the projection plane.

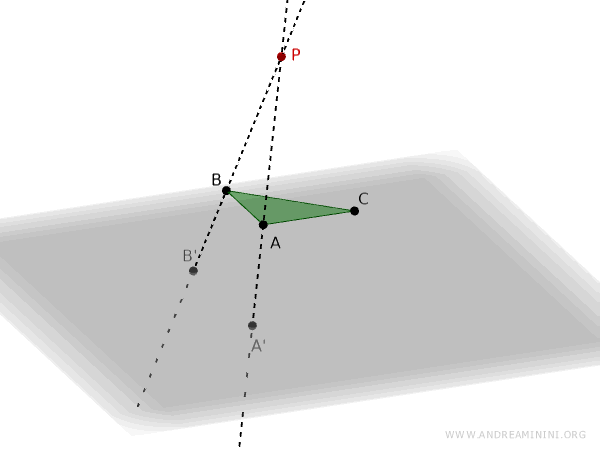
Finally, we draw a line through points P and C, which gives us point C' on the projection plane.

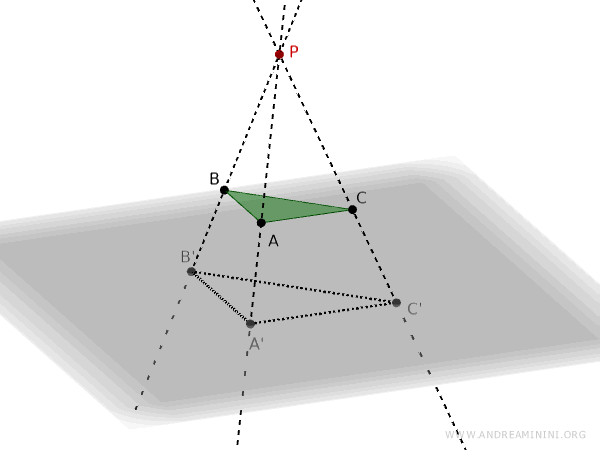
This process gives us the projection of triangle ABC onto the plane q from the projection center P.

Connecting points A', B', and C' on the plane results in the projection of triangle ABC.

The final outcome, of course, depends on the shape (or solid), the choice of projection point P, and the plane (distance, angle, etc.).

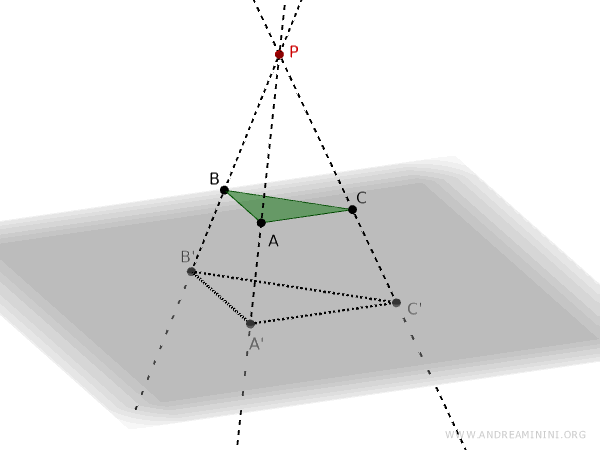
Here’s another example of a projection.

However, certain invariants can already be observed. For instance, the projection of a line segment is another line segment. The projection of a convex shape is another convex shape. The projection of a triangle is another triangle. These are just a few of the invariants that can be noticed in the example we’ve just discussed.

And so on.