Affine Transformations

An affine transformation (or affinity) is a geometric mapping that preserves the alignment of points and the parallelism of lines, but not necessarily distances or angles.

In essence, an affine transformation can translate, rotate, scale, reflect, or shear a figure, as long as straight lines remain straight and parallel lines remain parallel. The relative order of points along a line is always maintained.

The alignment of points and the parallelism of lines are the fundamental invariants of affine transformations.

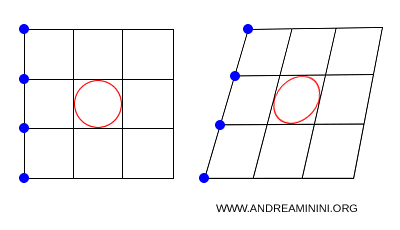
In general, lengths, angles, and areas are not preserved.

The overall shape of a figure is not invariant under an affine transformation. For instance, a right triangle can be mapped into an acute or obtuse triangle.

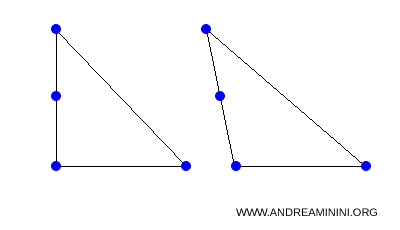
Mathematically, an affine transformation is a function that maps points, lines, and figures from one plane or space to another while keeping parallel lines parallel.

$$ \mathbf{y} = A\mathbf{x} + \mathbf{b} $$

Here \( \mathbf{x} \) is the vector of initial coordinates (before transformation), \( A \) is the matrix representing the linear part of the transformation (rotations, scalings, reflections, etc.), and \( \mathbf{b} \) is the translation vector that shifts the figure as a whole.

Affine transformations may or may not be isometries, meaning they can preserve distances and angles or alter them. What always remains invariant is the parallelism of lines and the collinearity of points.

A Practical Example

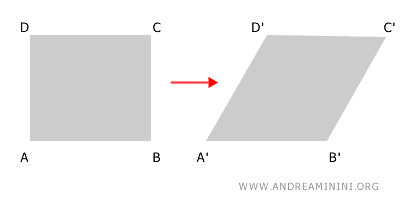
Example 1: Non-Isometric Affinity

This transformation is affine because it preserves both the parallelism of lines and the alignment of points.

However, it is non-isometric, since it does not preserve congruence: segment lengths and angle measures change.

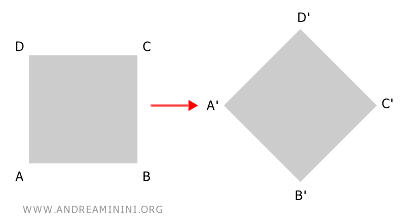
Example 2: Isometric Affinity

This is an isometric affinity, obtained by combining a translation with a rotation.

Here, the transformation preserves parallelism, collinearity, and the congruence of corresponding lengths and angles.

The Affinity Ratio

In an affine transformation, the ratio between the areas of two corresponding figures is constant: $$ \frac{A_{S'}}{A_S} = k $$. Here, $ S $ is a plane figure and $ S' $ is its affine image. The constant \( k \) is called the affinity ratio.

If $ k = 1 $, then $ A_{S'} = A_S $, meaning the transformation preserves area.

Affine transformations that preserve area are called equiaffinities or area-preserving affinities.

Example

Consider a square \(S\) with side length 2. Its area is:

\( A_S = 2^2 = 4. \)

Apply an affine transformation that stretches the horizontal coordinates by a factor of two while keeping the vertical coordinates unchanged. Analytically, this transformation is defined by:

\[ \begin{cases} x' = 2x \\ \\ y' = y \end{cases} \]

The new figure \(S'\) is a rectangle with base 4 and height 2, giving an area of:

\( A_{S'} = 4 \times 2 = 8. \)

Hence:

\[ \frac{A_{S'}}{A_S} = \frac{8}{4} = 2 = k. \]

The affinity ratio is therefore \(k = 2\).

Note. If the transformation consisted only of a rotation or translation (with no scaling), we would have \(k = 1\), and the area would remain unchanged. In that case, the transformation would be equiaffine.

Affine Transformation Equations

In analytic geometry, an affine transformation is defined by a pair of linear equations that map each point \( (x, y) \) in the plane to a new point \( (x', y') \):

\[
\begin{cases}
x' = a x + b y + c \\ \\
y' = a' x + b' y + c'
\end{cases}
\]

The coefficients \( a, b, a', b' \) determine how the plane is transformed through operations such as rotation, scaling, or shear, while \( c \) and \( c' \) represent translation components that shift the figure in the plane.

The condition \( ab' - a'b \neq 0 \) ensures that the determinant of the linear part of the transformation matrix is nonzero:

\[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} \ne 0 \]

This condition is essential because it guarantees that the mapping is invertible, meaning the transformation establishes a one-to-one correspondence between points in the original and transformed planes.

The sign of the determinant determines whether the affine transformation is direct or indirect.

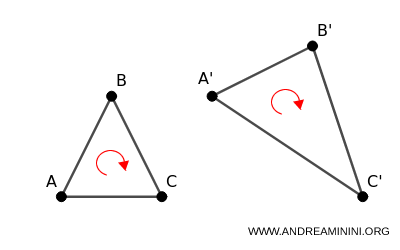
• Direct affine transformation
  When the determinant is positive, the transformation preserves the orientation of the points \( A, B, C \). In this case, it is called a "direct" affine transformation. \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} > 0 \]
  
• Indirect affine transformation
  When the determinant is negative, the transformation reverses the orientation of the points \( A, B, C \), and it is referred to as an "indirect" affine transformation. \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} < 0 \]
  

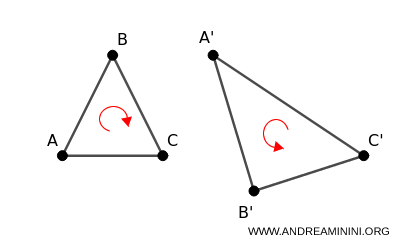
In summary, a direct affine transformation modifies the figure without reflecting it, while an indirect one both distorts and reflects it across an axis.

More generally, the sign of the determinant serves as an orientation indicator for the coordinate system after the transformation. A positive determinant preserves the original orientation, whereas a negative determinant reverses it.

Example

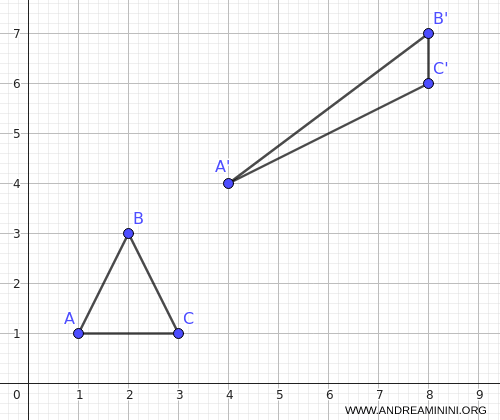
Consider a triangle with vertices \( A(1, 1), B(2, 3), C(3, 1) \).

We apply the following affine transformation:

\[
\begin{cases}
x' = 2x + y + 1 \\ \\
y' = x + y + 2
\end{cases}
\]

Compute the determinant of the linear transformation matrix:

\[
D =
\begin{vmatrix}
2 & 1 \\
1 & 1
\end{vmatrix}
= 2 \cdot 1 - 1 \cdot 1 = 1 > 0
\]

Since the determinant is positive, the affine transformation is direct and preserves the original orientation of the triangle.

We now compute the images of the three vertices:

• For A(1, 1): \[ x'_A = 2(1) + 1 + 1 = 4 \] \[ y'_A = 1 + 1 + 2 = 4 \] Thus, the image is \( A′(4, 4) \).
• For B(2, 3): \[ x'_B = 2(2) + 3 + 1 = 8 \] \[ y'_B = 2 + 3 + 2 = 7 \] Thus, the image is \( B′(8, 7) \).
• For C(3, 1): \[ x'_C = 2(3) + 1 + 1 = 8 \] \[ y'_C = 3 + 1 + 2 = 6 \] Thus, the image is \( C′(8, 6) \).

The transformed triangle therefore has vertices \( A′(4, 4), B′(8, 7), C′(8, 6) \).

The area changes due to scaling, but the vertex order - and hence the orientation - remains the same because the determinant is positive.

This affine transformation applies a combination of linear deformation and translation to the triangle, without reflection.

Example 2

Now, consider again the same triangle \( A(1, 1), B(2, 3), C(3, 1) \).

This time, we apply an indirect affine transformation, characterized by a negative determinant.

\[
\begin{cases}
x' = x + 2y \\ \\
y' = 3x + y
\end{cases}
\]

Calculate the determinant of the linear transformation:

\[
D =
\begin{vmatrix}
1 & 2 \\
3 & 1
\end{vmatrix}
= 1\cdot1 - 3\cdot2 = 1 - 6 = -5 < 0
\]

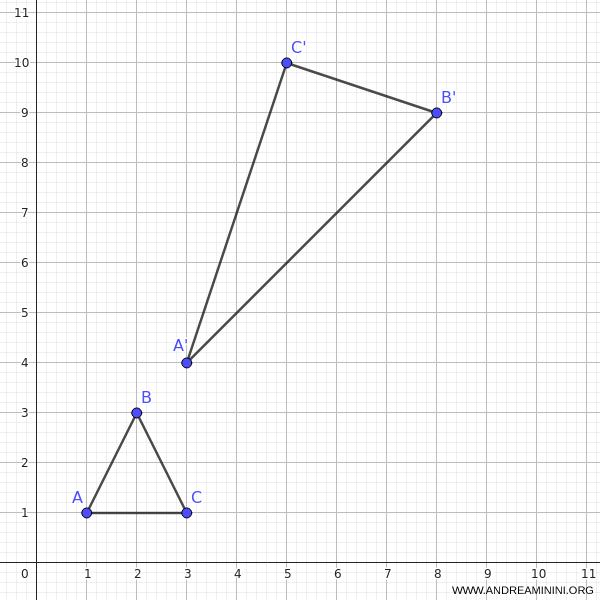
Since the determinant is negative, this affine transformation is indirect and reverses the triangle's orientation.

Compute the images of the vertices:

• For A(1, 1): \[ x'_A = 1 + 2(1) = 3 \] \[ y'_A = 3(1) + 1 = 4 \] Hence, the image is \( A′(3, 4) \).
• For B(2, 3): \[ x'_B = 2 + 2(3) = 8 \] \[ y'_B = 3(2) + 3 = 9 \] Hence, the image is \( B′(8, 9) \).
• For C(3, 1): \[ x'_C = 3 + 2(1) = 5 \] \[ y'_C = 3(3) + 1 = 10 \] Hence, the image is \( C′(5, 10) \).

The transformed triangle thus has vertices \( A′(3, 4), B′(8, 9), C′(5, 10) \).

Because the determinant is negative, the resulting triangle is reflected relative to the original, and the vertex orientation (clockwise versus counterclockwise) is inverted.

Fixed Points in Affine Transformations

In an affine transformation, there may exist one, none, or infinitely many fixed points, that is, points that remain invariant under the transformation.

An affine transformation with exactly one fixed point is called a central affinity or center-affine transformation.

As a direct corollary, if an affine transformation admits two distinct fixed points, then it necessarily has infinitely many, since any two fixed points determine a straight line consisting entirely of fixed points.

Proof

Consider the general form of an affine transformation:

\[ \begin{cases} x' = a x + b y + c \\ y' = a' x + b' y + c' \end{cases} \]

If a point \( (x', y') \) is fixed, then \( x' = x \) and \( y' = y \). Substituting these relations gives:

\[ \begin{cases} x = a x + b y + c \\ y = a' x + b' y + c' \end{cases} \]

\[ \begin{cases} (a - 1)x + b y + c = 0 \\ a' x + (b' - 1)y + c' = 0 \end{cases} \]

\[ \begin{cases} (a - 1)x + b y = -c \\ a' x + (b' - 1)y = -c' \end{cases} \]

This linear system of equations may have three types of solutions:

• Consistent and independent: a unique solution exists, meaning there is exactly one fixed point.
• Inconsistent: no solution exists, meaning there are no fixed points.
• Dependent: infinitely many solutions exist, implying an infinite set of fixed points lying on a straight line.

This shows that an affine transformation can have one, none, or infinitely many fixed points, but never exactly two. If two or more fixed points exist, they define a continuous line of fixed points.

Further Remarks

Additional properties of affine transformations:

• Preservation of Parallelograms
  Since affine transformations maintain the parallelism of lines, any parallelogram is mapped to another parallelogram, which may be translated, rotated, scaled, or sheared, but its opposite sides remain parallel.
• Incidence of Lines
  If two lines intersect at a point $ P $, their images under an affine transformation intersect at a point $ P' $, the image of $ P $.
• Conic Sections
  An affine transformation preserves the type of a conic section: an ellipse maps to another ellipse, a parabola to another parabola, and a hyperbola to another hyperbola. In particular, a circle - considered a special case of an ellipse - is generally transformed into an ellipse.
• Isometries and Similarities as Subsets
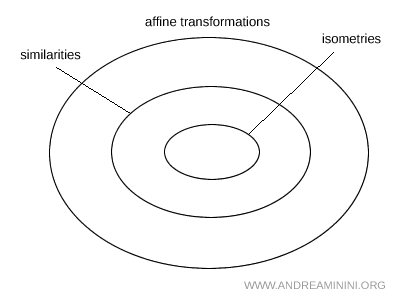
  Isometries and similarities are special cases of affine transformations. The set of all affine transformations includes similarities as a subset, and within those, the isometries.
  
• Dilations as affine transformations
  A dilation is a specific instance of an affine transformation in which the scaling factors \( h \) and \( k \) are both nonzero, that is \( h \ne 0 \) and \( k \ne 0 \). $$ \begin{cases} x' = h x + p \\[4pt] y' = k y + q \end{cases} $$ The parameters \( h \) and \( k \) act as the principal scale factors that stretch or compress the figure along the coordinate axes. The factor \( h \) governs scaling in the \( x \) direction, while \( k \) serves the same role along the \( y \) axis.

  Observation. Because both scaling factors are nonzero, the determinant of the associated linear matrix is also nonzero. This ensures that the mapping qualifies as a genuine affine transformation: $$ \begin{vmatrix} h & 0 \\ 0 & k \end{vmatrix} = hk \ne 0 $$

• Isometric Affinities: Conditions for an Isometry
  An affine transformation is an isometry precisely when the following conditions are satisfied: $$ \begin{cases} a^2 + a'^2 = 1 \\ b^2 + b'^2 = 1 \\ ab + a'b' = 0 \end{cases} $$
• Affine transformations and similarity: conditions for similarity
  An affine transformation qualifies as a similarity transformation exactly when the following conditions are met: $$ a^2 + a'^2 = b^2 + b'^2 $$ $$ ab + a'b' = 0 $$ Under these constraints, the similarity ratio is $$ k = \sqrt{a^2 + a'^2} = \sqrt{b^2 + b'^2} $$

And so on.