Angles

An angle is the part of a plane between two rays that share a common starting point.

The two rays are called the sides of the angle.

The common starting point is known as the vertex of the angle.

The measure of the angle between the two rays can be expressed in degrees using the sexagesimal system or in radians.

To denote the measure of an angle, we often use a lowercase Greek letter (e.g., α, β, γ, etc.).

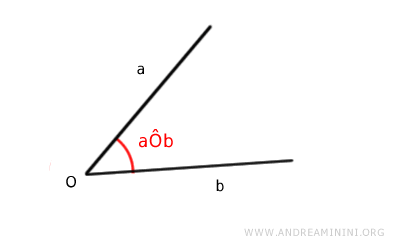
Alternatively, the notation aÔb can be used, where "a" and "b" represent the sides, and "Ô" is the vertex of the angle.

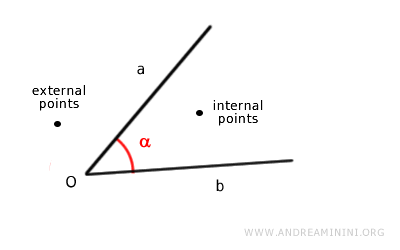
All points located between the two sides of the angle that do not lie on the rays are called internal points of the angle.

All other points are referred to as external points of the angle.

Measuring Angles

To measure the measure of the angle, a numerical value is assigned to each angle according to a measurement system.

The primary systems for measuring angles are degrees (sexagesimal system) and radians.

• Measurement in Degrees
  This method divides a circle (full angle) into 360 equal parts called degrees.
• Measurement in Radians
  A radian is an angle that subtends an arc equal in length to the radius. There are 2π radians in a full circle, approximately 6.28 radians.

Angle measurements allow us to classify all angles in the plane into sets/classes of congruent angles.

Each class represents a single measure.

Specifically, two or more angles are called congruent angles if they have the same measure.

Therefore, congruent angles belong to the same equivalence class.

Note: Congruent angles do not need to share the same points in the plane or have the same orientation in space. What matters for the congruence relationship is that they have the same measure.

To compare two angles, you need to place the first angle over the second one with a rigid motion, making sure that one side of each angle aligns and that both angles are positioned on the same side of the shared line.

If the two angles align perfectly, then they are congruent $ \alpha \cong \beta $. If not, the angles have different measures.

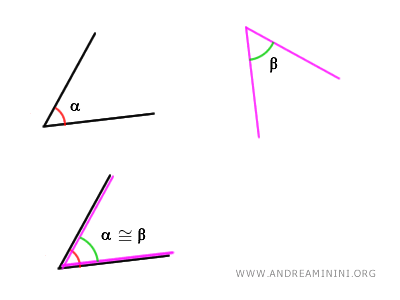
The length of the sides doesn’t matter, as the size of the angles isn’t determined by the length of their sides.

Types of Angles

There are various types of angles.

• Concave Angles
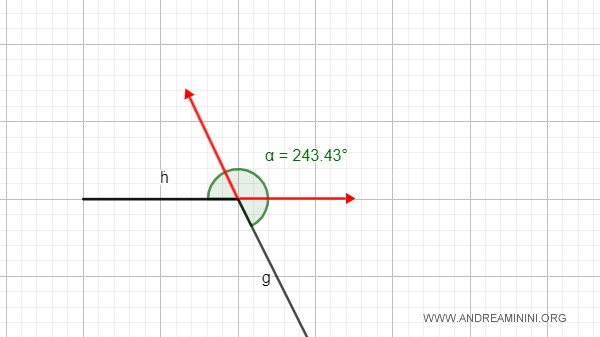
  An angle is concave if it contains the extensions of its sides.
  
• Convex Angles
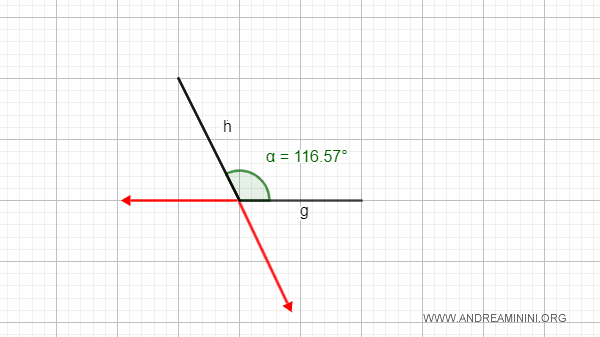
  An angle is convex if it does not contain the extensions of its sides.
  
• Right Angle
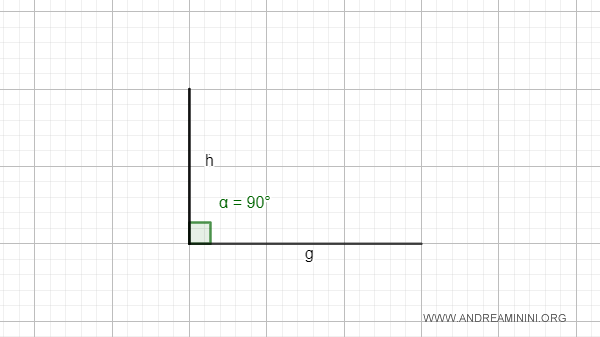
  A right angle is formed when the lines are perpendicular to each other, creating four congruent angles. A right angle measures 90° (π/2 radians).
  

  Note: Two angles are congruent when they have the same measure.

• Full Angle
  A full angle occurs when the sides coincide and the angle contains all points in the plane. It measures 360° (2π radians).
  

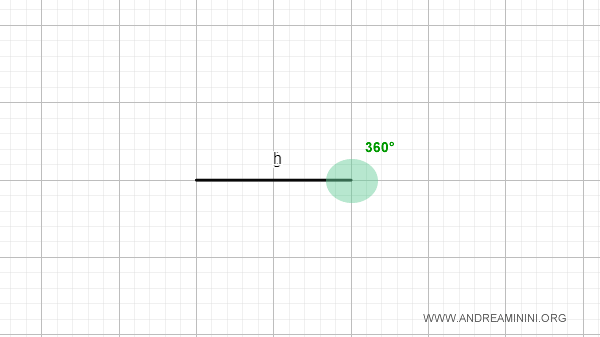
  Note: In a full angle, the sides are coincident rays.

• Zero Angle
  A zero angle occurs when the sides coincide and the angle contains only the points on the rays. It measures 0° (zero radians).

Directed Angles

By convention, an angle is positive when the rotation is counterclockwise.

The initial side associated with the zero angle is the positive x-axis.

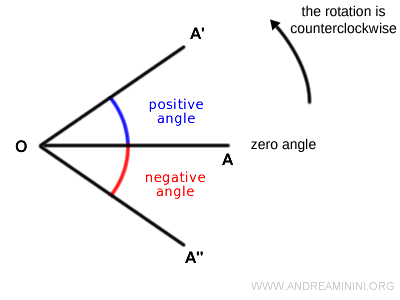
Conversely, if the rotation is clockwise, the angle is negative.

This convention is used in almost all mathematics and physics texts.

Adjacent and Consecutive Angles

Adjacent and consecutive angles differ in their positions relative to a line or a point.

• Consecutive Angles
  Two angles are consecutive if they share a vertex and a side.
  
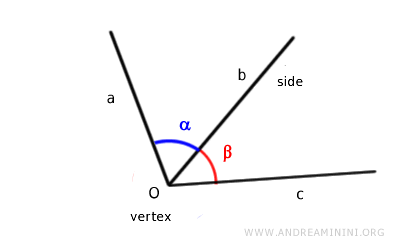
• Adjacent Angles
  Two angles are adjacent if they share a vertex and a side, and their non-common sides lie on the same line.
  

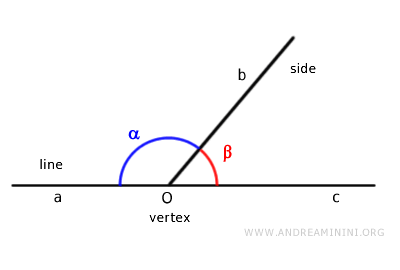
  Note: Adjacent angles are also consecutive, but the reverse is not necessarily true. The sum of two adjacent angles is always 180°, which is a straight angle.

Concave and Convex Angles

Angles can be either concave or convex.

• Concave Angles
  An angle is defined as concave when it includes the extensions of its sides, except for the full angle.
  
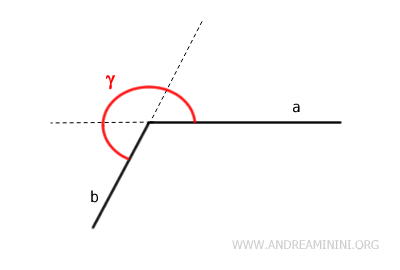
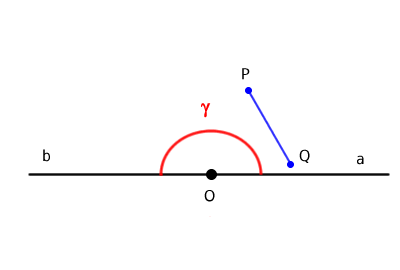
  A concave angle can also be identified by selecting two internal points, P and Q, and drawing a segment between them. If this segment is not entirely contained within the angle, meaning it includes external points, then the angle is concave.
  

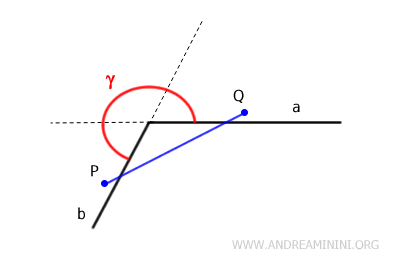
  Note: A full angle (360 degrees) is not considered concave because any two internal points selected will have a segment connecting them entirely within the angle. It has no external points.

• Convex Angles
  An angle is defined as convex when it does not include the extensions of its sides.
  
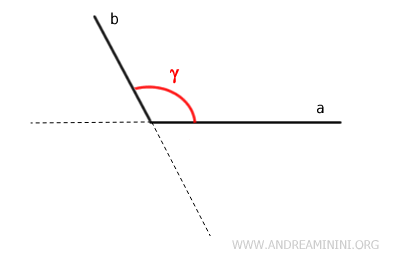
  In this case, if any two points, P and Q, are taken inside the angle and connected with a segment, this segment remains entirely within the angle. In other words, the segment has no external points.
  
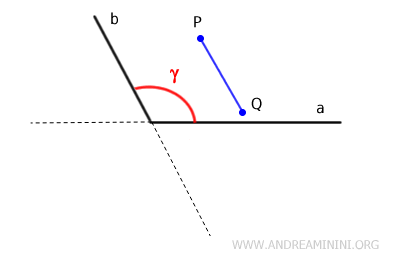
  Therefore, all angles from 0 to 180° are convex angles.
  

  Note: A straight angle (180°) is considered convex because the points on the sides of the straight angle are not internal points. Thus, any two internal points selected will not intersect the sides or their extensions.
  

And so on