Alternate Angles

Given two lines "r" and "s" and a transversal "t", two angles are called alternate angles if they do not share the same vertex and lie on opposite sides of the transversal.

Alternate angles can be:

• Interior Alternate Angles
  if they are between the lines "r" and "s".
• Exterior Alternate Angles
  if they are outside the lines "r" and "s".

A Practical Example

Let's consider two lines "r" and "s".

A transversal "t" intersects these two lines at different points.

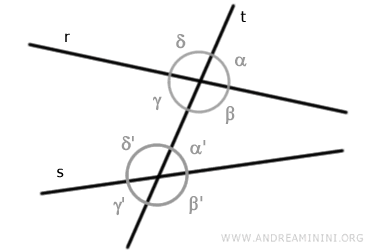
Two sets of angles are formed at the points of intersection.

The angles (β, δ') shown in red are interior alternate angles because they do not share the same vertex and are on opposite sides of the transversal "t".

They are considered interior because they lie between the lines "r" and "s".

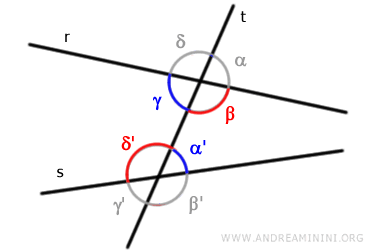
In the same way, the angles (γ, α') shown in blue are also interior alternate angles for the same reasons.

The angles (α, γ') shown in red are exterior alternate angles because they do not share the same vertex and are on opposite sides of the transversal "t".

They are called exterior because they lie outside the lines "r" and "s".

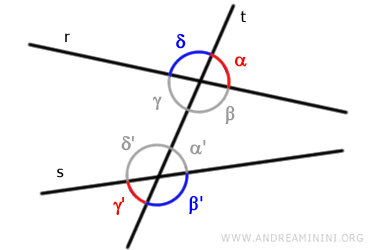
Similarly, the angles (β', δ) shown in blue are exterior alternate angles for the same reasons.

And so on.