Supplementary, Complementary, and Explementary Angles

Two angles are described as complementary, supplementary, or explementary based on whether their sum equals a right angle, a straight angle, or a full circle, respectively.

• Complementary Angles

  Two angles are complementary if their measures add up to 90 degrees (π/2 radians).
  

  Simply put, if the sum of two angles equals a right angle, they are complementary.

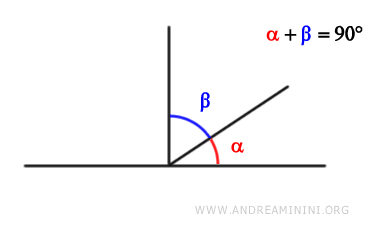
  For instance, if one angle measures 30 degrees and the other measures 60 degrees $$ \alpha=30° $$ $$ \beta=60° $$ they are complementary because their sum is 90 degrees $$ \alpha+\beta = 30° + 60° = 90° $$.

• Supplementary Angles

  Two angles are supplementary if their measures add up to 180 degrees (π radians).
  

  In other words, if the sum of two angles equals a straight angle, they are supplementary.

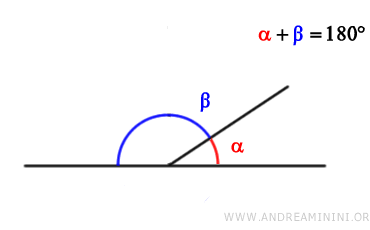
  For example, if one angle is 120 degrees and the other is 60 degrees $$ \alpha=120° $$ $$ \beta=60° $$ they are supplementary because their sum is 180 degrees $$ \alpha+\beta = 120° + 60° = 180° $$.

• Explementary Angles

  Two angles are explementary if their measures add up to 360 degrees (2π radians).
  

  Simply put, if the sum of two angles forms a full circle, they are explementary.

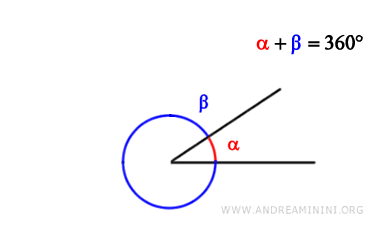
  For instance, if one angle is 270 degrees and the other is 90 degrees $$ \alpha=270° $$ $$ \beta=90° $$ they are explementary because their sum is 360 degrees $$ \alpha+\beta = 270° + 90° = 360° $$.

In summary, complementary, supplementary, and explementary angles are classified by the sum of their measures. Complementary angles sum to 90°, supplementary angles to 180°, and explementary angles to 360°.

These definitions only apply to pairs of angles.

Therefore, a single angle cannot be described as supplementary, complementary, or explementary without reference to another angle.

And so forth.