Explementary Angles

Explementary angles are two angles whose measures add up to 360 degrees, forming a complete circle.

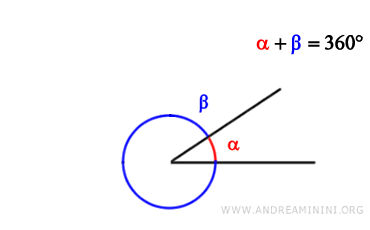
In other words, two explementary angles create a full rotation around a circle.

A Practical Example

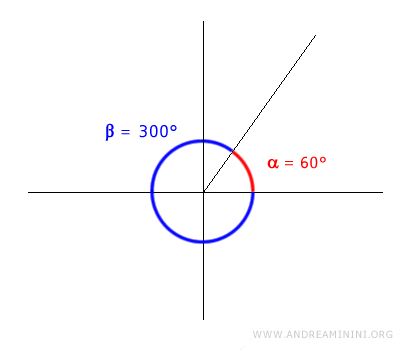
Let's consider two angles. One angle, alpha, measures 60°, and another angle, beta, measures 300°.

$$ \alpha = 60° $$

$$ \beta = 300° $$

If we add these two angles together, we get a total of 360 degrees.

$$ \alpha + \beta = 60° + 300° = 360° $$

This means that these two angles are explementary.

Another example could be a right angle of 90 degrees and an angle of 270 degrees. In this case, the sum of the measures is 360 degrees, making these two angles explementary. $$ 90° + 270° = 360° $$ Similarly, any other combination of angles that adds up to a full circle are explementary. $$ \alpha + \beta = 360° $$

Notes

Here are some additional notes on explementary angles:

• The definition of explementary angles applies only to pairs of angles. Therefore, a single angle cannot be "explementary."
• Explementary angles belong to the category of angles associated by their measures, which includes complementary angles (sum is 90°), supplementary angles (sum is 180°), and explementary angles (sum is 360°).
• Given any angle alpha, you can find the other angle beta that forms an explementary pair by subtracting alpha from 360°. $$ \beta = 360° - \alpha $$ For example, if angle alpha is 120°, the other angle in the explementary pair would be 240°. $$ \beta = 360° - 120° = 240° $$
• If a concave angle and a convex angle share the same sides and vertex, then they are an explementary pair.

And so on.