Eudoxus-Archimedes Postulate on Angles

The Eudoxus-Archimedes postulate states that for any two non-congruent angles with non-zero measures, it is always possible to find a multiple of the smaller angle that exceeds the larger angle.

This principle is fundamental in Euclidean geometry.

The postulate is named after the ancient mathematicians Eudoxus and Archimedes, who proposed and utilized it.

Note: This applies the well-known Eudoxus-Archimedes postulate on segments to angles.

A Practical Example

Consider two angles, alpha and beta.

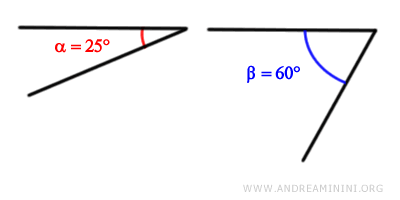
Both angles have non-zero measures.

$$ \alpha = 25° $$

$$ \beta = 60° $$

Moreover, the two angles are non-congruent because angle beta has a greater measure than angle alpha.

In this case, there exists a multiple of the smaller angle (alpha) that exceeds the larger angle (beta).

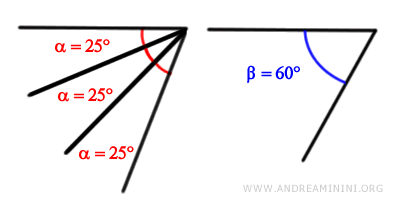
This multiple is 3 times angle alpha:

$$ 3 \cdot \alpha > \beta $$

$$ 3 \cdot 25° > 60° $$

$$ 75° > 60° $$

Therefore, regardless of the measures of two non-congruent angles, as long as they are non-zero, it is always possible to find a multiple of the smaller angle that exceeds the measure of the larger angle.

And so on.