Eudoxus-Archimedes Postulate of Segments

According to the Eudoxus-Archimedes Postulate, given two segments of different lengths (non-congruent) and non-zero, it is always possible to find a multiple of the shorter segment that exceeds the longer segment.

This principle is also known as the Archimedean principle because Archimedes used it in various geometric proofs.

Essentially, the postulate asserts that you can always "scale up" a shorter segment to exceed a longer one by multiplying it a finite number of times.

Note: This is a fundamental concept in mathematics, particularly in geometry and calculus. The Archimedean principle underpins many areas of mathematics, including real numbers and the concept of limits, which are essential in calculus.

A Practical Example

Let's consider two segments, AB and CD.

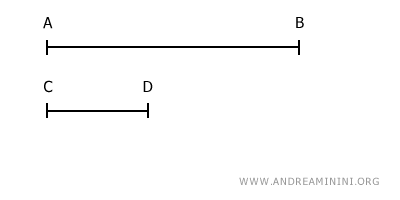
Both segments have a positive length (non-zero) and are different from each other, meaning they are non-congruent.

Segment AB is longer than segment CD.

We multiply the shorter segment CD by two.

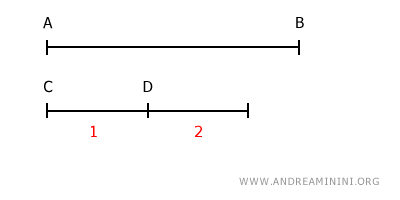
The resulting segment is still shorter than AB.

So, let's try multiplying the shorter segment CD by three.

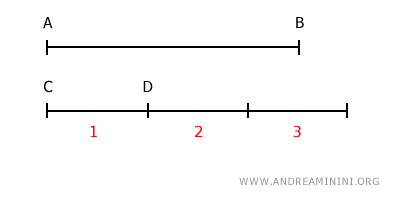
This time, the resulting segment exceeds the length of segment AB.

Therefore, the segment that is three times the length of the shorter segment CD exceeds the longer segment AB.

And so on.