Angle Measurement

Angle measurement refers to the size of the opening between two lines or rays, known as the sides of the angle, which meet at a common point called the vertex.

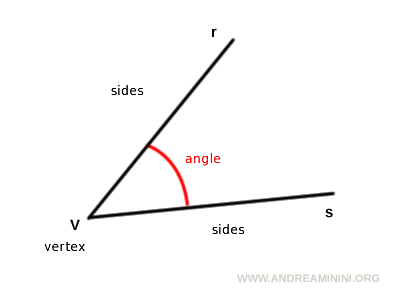
It indicates the size of an angle.

Angles are measured in degrees, ranging from 0° to 360°, or in radians.

Other meanings of measurement. In geometry, the term measurement generally refers to the size of an angle. However, it has other meanings too. For instance, in mathematics, it can indicate the difference between the two extremes of an interval, class, or set. In this case, measurement refers to the difference between the maximum and minimum values of a set.

Units of Angle Measurement

Angle measurement can be expressed in different units, including degrees, radians, and revolutions.

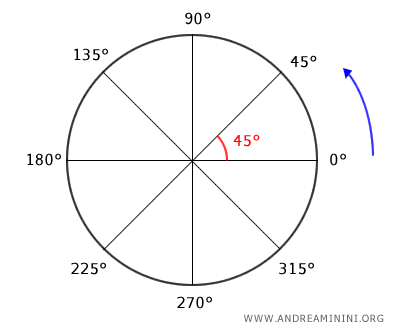
• Degrees
  This is the most familiar unit in plane geometry, where a full circle is 360 degrees. A straight angle is 180°, and a right angle, which is half of a straight angle, is 90 degrees.
  
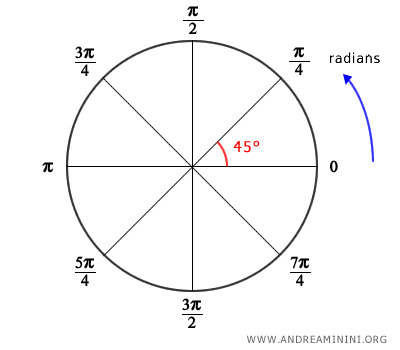
• Radians
  In mathematics and physics, angles are often measured in radians. A radian is defined as the angle formed when the arc length is equal to the radius of the circle. Hence, there are 2π radians in a full circle (approximately 6.283 radians).
  
• Revolutions
  Sometimes, angles are measured in revolutions, where one full revolution equals a complete circle and half a revolution equals a semicircle. Thus, a straight angle is equivalent to 1/2 revolution and a right angle is equivalent to 1/4 revolution.
  

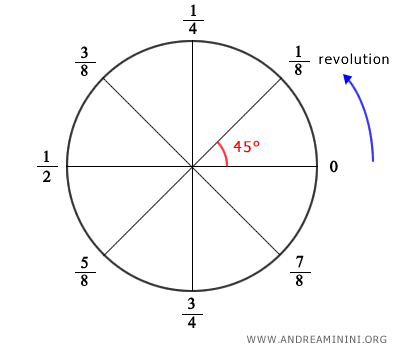
For comparison, a full revolution equals 360 degrees and 2π radians.

A Practical Example

To understand angle measurement, it is useful to imagine a clock.

The hour and minute hands are two sides (rays) that form angles of various sizes.

For example, when the hands are at 3:00, they form a right angle of 90 degrees.

Similarly, an angle of 180 degrees, called a straight angle, is represented by the hands at 6:00.

This is exactly twice the previous angle.

An angle of 270 degrees is represented by the hands at 9:00, exactly three times the size of a right angle.

A clock is one of the simplest ways to understand angle measurement.

No matter the size of the clock, whether small or as large as Big Ben, the angle between the hands is measured the same way.

Equivalence Classes

Angles with the same measurement are called congruent and belong to the same equivalence class.

For example, two angles of 45 degrees belong to the same equivalence class.

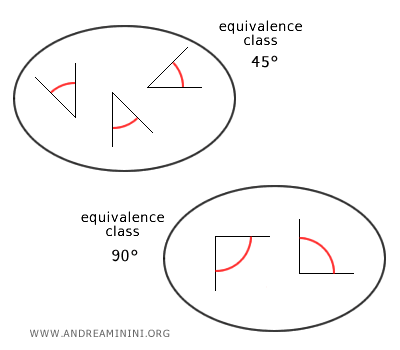
An angle of 45 degrees and an angle of 90 degrees, however, belong to different equivalence classes.

From this, we can deduce that it is always possible to compare two angles.

Moreover, the sum of two angles is not an internal operation because the result can belong to a different equivalence class.

For example, the sum of two congruent angles measuring 45 degrees results in a sum of 90 degrees, which belongs to a different equivalence class.

And so on.