Adjacent Angles

Adjacent angles are two angles that share the same vertex and one side, but do not overlap.
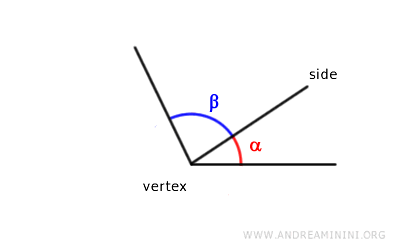
example of adjacent angles

In geometry, adjacent angles share a side but do not overlap in their interior regions.

Adjacent angles are a type of associated angles by position.

The sum of two adjacent angles can vary and may form either a convex or concave angle, depending on their measures.

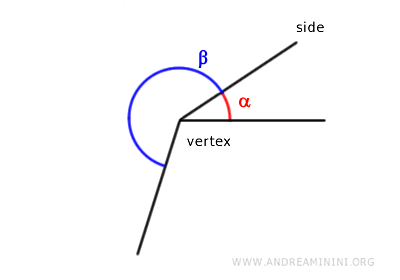
an example of adjacent angles between a convex and a concave angle

For adjacent angles, the other sides do not need to be aligned.

The difference between adjacent and linear pair of angles. When the non-shared sides are also aligned, meaning they lie on the same line, the adjacent angles are called linear pair of angles, and their sum is always equal to a straight angle (180°).
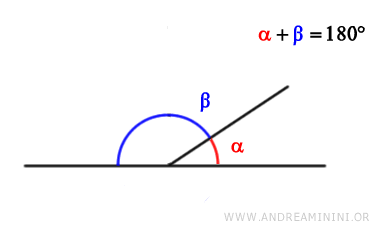
example of a linear pair of angles
Therefore, a linear pair of angles is always also an adjacent angle. However, an adjacent angle is not necessarily a linear pair, because the opposite sides might not be aligned.

And so on.