Complementary Angles

A pair of angles are called complementary angles if their sum is 90° or π/2 radians.

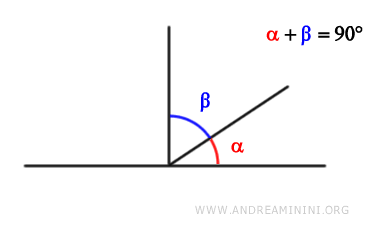
The term "complementary" comes from the Latin word "complementum," which means "that which completes."

In this case, one angle completes the other to form a right angle, which is 90 degrees.

Note: It doesn't matter what the measures of the two angles are, as long as their sum is 90°.

A Practical Example

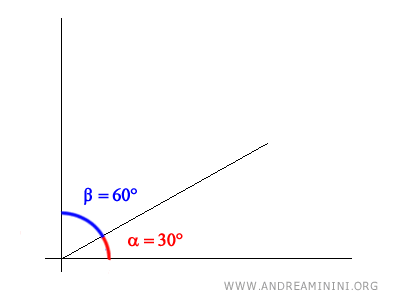
For instance, consider two angles, alpha and beta:

$$ \alpha = 30° $$

$$ \beta = 60° $$

These angles are complementary because their sum is 90°.

$$ \alpha + \beta = 30° + 60° = 90° $$

Graphically:

Every angle has a complementary angle.

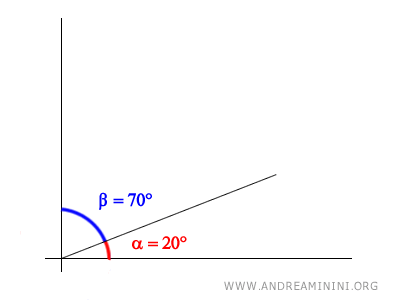
For example, consider the angle:

$$ \alpha = 20° $$

To find the complementary angle, subtract the given angle from 90°.

$$ \beta = 90° - \alpha $$

$$ \beta = 90° - 20° $$

$$ \beta = 70° $$

In this case, the complementary angle is 70°.

Observations

Some properties and observations about complementary angles:

• If two angles a and b are complementary to the same angle c, then a and b are congruent. $$ \alpha + \gamma = 90° \ , \ \beta + \gamma = 90° \ \Longrightarrow \ \alpha \cong \beta $$

  Proof: Since the sum of the angles is constant (90 degrees), if one angle is fixed, the other must be the same for both pairs of angles. Knowing that $$ \alpha + \gamma = 90° $$ and $$ \beta + \gamma = 90° $$ we find gamma by subtracting beta from 90 degrees: $$ \gamma = 90° - \beta $$ Then we substitute γ=90-β in the equation α+γ=90: $$ \alpha + \gamma = 90° $$ $$ \alpha + ( 90° - \beta ) = 90° $$ $$ \require{cancel} \alpha + \cancel{90°} - \beta = \cancel{90°} $$ $$ \alpha - \beta = 0° $$ The difference between alpha and beta is zero, meaning they have the same measure. Therefore, alpha and beta are congruent. $$ \alpha \cong \beta $$

• If one angle is complementary to a second angle, and the second angle is complementary to a third angle, then the first and third angles are equal. $$ \alpha + \beta = 90° \ , \ \beta + \gamma = 90° \ \Longrightarrow \ \alpha \cong \gamma $$

  Proof: Knowing that $$ \alpha + \beta = 90° $$ and $$ \beta + \gamma = 90° $$ we find beta by subtracting gamma from 90 degrees: $$ \beta = 90° - \gamma $$ Then we substitute β=90-γ in the equation α+β=90: $$ \alpha + \beta = 90° $$ $$ \alpha + ( 90° - \gamma ) = 90° $$ $$ \require{cancel} \alpha + \cancel{90°} - \gamma = \cancel{90°} $$ $$ \alpha - \gamma = 0° $$ If the difference between alpha and gamma is zero, they have the same measure. Therefore, they are congruent angles. $$ \alpha \cong \gamma $$

• If two angles, α and β, are complementary to the same angle, γ, then α and β are congruent, meaning they have the same measure.

  Proof: Consider two pairs of complementary angles: $$ \alpha + \gamma = 90° $$ $$ \beta + \gamma = 90° $$ We find alpha and beta by subtracting from 90 degrees: $$ \alpha = 90° - \gamma $$ $$ \beta = 90° - \gamma $$ This shows that α and β have the same measure. $$ \alpha = \beta = 90° - \gamma $$ Thus, α and β are congruent.

• Two complementary angles, $ \alpha $ and $ \beta $, corresponding to two congruent angles, $ \gamma_1 \cong \gamma_2 $, are themselves congruent: $ \alpha \cong \beta $. 

  Proof. By definition, complementary angles add up to a right angle. Therefore: $$ \alpha + \gamma_1 = 90^\circ $$ $$ \alpha + \gamma_2 = 90^\circ $$ Since the gamma angles are congruent: $$ \gamma_1 \cong \gamma_2 $$ We can express $ \alpha $ and $ \beta $ as: $$ \alpha = 90^\circ - \gamma_1 $$ $$ \beta = 90^\circ - \gamma_2 $$ Given that $ \gamma_1 \cong \gamma_2 $, it follows that: $$ \alpha = 90^\circ - \gamma_1 $$ $$ \beta = 90^\circ - \gamma_1 $$ Thus, $ \alpha $ and $ \beta $ are congruent: $$ \alpha \cong \beta \cong 90^\circ - \gamma_1 $$

• The sine of an angle is equal to the cosine of its complementary angle. $$ \alpha + \beta = 90° \Longrightarrow \sin( \alpha) = \cos( \beta) $$

  For example, angles 70° and 20° are complementary because their sum is a right angle: $$ 70° + 20° = 90° $$ The cosine of 70° is equal to the sine of 20°: $$ \cos(70°) = \sin(20°) = 0.94 $$ This occurs because, in trigonometry, the relationship between complementary angles is fundamental. Trigonometric functions of complementary angles are closely related.
  
  Proof: Consider the unit circle and an angle alpha (α) that forms a right triangle OAB.
  
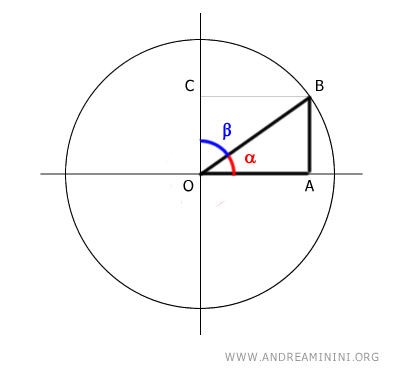
  The sine of angle alpha (α) is the ratio of the opposite side (AB) to the hypotenuse (OB): $$ \sin \alpha = \frac{ \overline{AB} }{ \overline{OB} } $$ The cosine of angle alpha (α) is the ratio of the adjacent side (OA) to the hypotenuse (OB): $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } $$ The complementary angle to alpha (α) is beta (β): $$ \alpha + \beta = 90° $$ Knowing that segments OA and CB are congruent: $$ \overline{OA} \cong \overline{CB} $$ we can also find the cosine by the ratio CB/OB: $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } = \frac{ \overline{CB} }{ \overline{OB} } $$ If we consider the triangle OBC, the purple triangle, the segment CB is opposite angle beta (β).
  
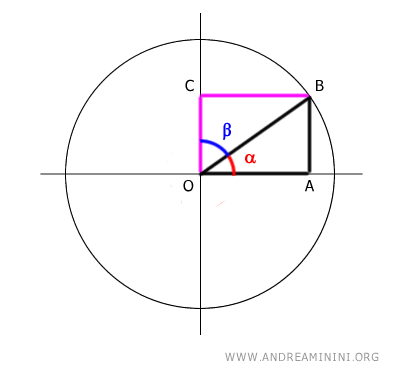
  Therefore, the ratio CB/OB is the sine of angle beta: $$ \cos \alpha = \frac{ \overline{OA} }{ \overline{OB} } = \frac{ \overline{CB} }{ \overline{OB} } = \sin \beta $$ Consequently, the cosine of angle alpha (α) is equal to the sine of its complementary angle beta (β): $$ \cos \alpha = \sin \beta $$ Additionally, knowing that segments AB and OC are congruent: $$ \overline{AB} = \overline{OC} $$ Following similar reasoning: $$ \sin \alpha = \frac{ \overline{AB} }{ \overline{OB} } = \frac{ \overline{OC} }{ \overline{OB} } = \cos \beta $$ we conclude that the sine of angle alpha (α) is equal to the cosine of its complementary angle beta (β): $$ \sin \alpha = \cos \beta $$ This is what we wanted to prove.

Complementary angles are a key concept in geometry and have many practical applications.

For instance, they are used in the design and construction of buildings and structures, as many structures use right angles. They are also used in navigation, cartography, and many other scientific disciplines.

And so on.