Space in Geometry

Space is a core concept in geometry. It consists of infinite planes and, broadly speaking, serves as the "container" for solid shapes.

In Euclidean geometry, "space" typically refers to three-dimensional space (x, y, z). This distinction is important because in mathematics, space can also extend beyond three dimensions.

Every solid geometric shape (e.g., cubes, rectangular prisms, spheres, etc.) can be thought of as a collection of points spread across different planes.

The branch of geometry that focuses on space is often called solid geometry.

Note: Solid geometric shapes are three-dimensional objects that allow us to explore not just their forms but also their geometric and physical properties. Unlike two-dimensional figures, which are limited to studying shape, three-dimensional figures provide additional depth for analysis.

In Euclidean geometry, space is commonly represented using Cartesian coordinates (x, y, z), which specify the positions of points across three dimensions: length, width, and height.

For instance, a cube is a solid shape with six square faces that can be described using coordinates to define its vertices in space.

The points of a cube lie on various planes that intersect at right angles.

 

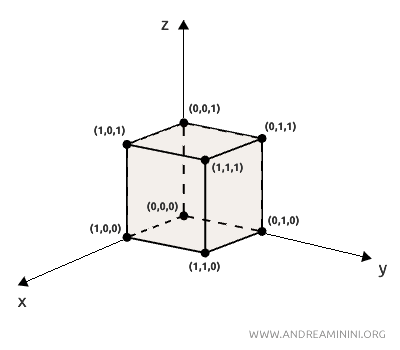
To represent a cube within a Cartesian system, its vertices could be assigned coordinates like (0, 0, 0), (0, 1, 0), (1, 1, 0), and so forth.

Lines in Space

Lines in space can either lie on the same plane or exist on different planes.

Two lines that lie on the same plane are known as coplanar lines. Depending on their relationship, they can either intersect at a single point or run parallel without ever meeting.

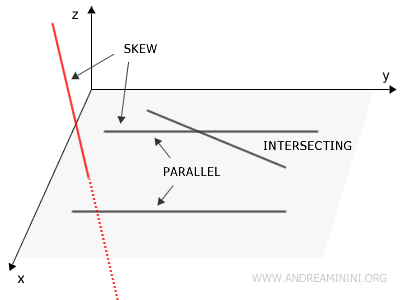
Lines that lie on different planes are referred to as skew lines, and they never intersect.

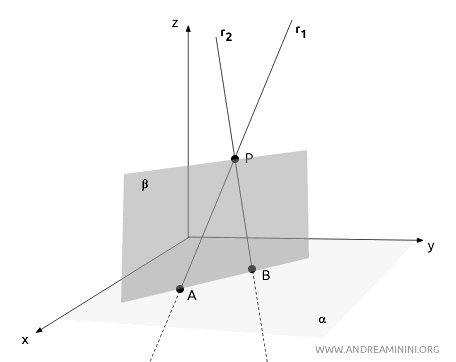
Why don’t skew lines intersect? Skew lines cannot intersect because, by definition, they do not lie on the same plane. To illustrate this, let’s assume—contrary to their definition—that two skew lines, r₁ and r₂, share a common point P.

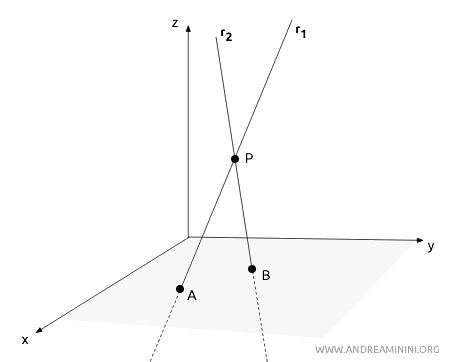
If this were the case, I could identify another point A on one line and a point B on the other, both distinct from P. These three points, P, A, and B, would define a single plane β that contains both lines. This would mean the lines are coplanar. However, the defining property of skew lines is that they are not coplanar. Therefore, if two lines intersect, they must belong to the same plane and cannot be skew lines. 

Planes in Space

Space consists of infinite planes, which can relate to one another in only two ways:

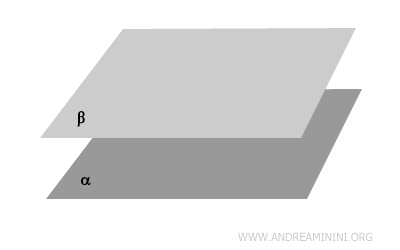
• Parallel Planes
  These planes do not intersect and remain equidistant at all points. A practical example is the floors of different levels in a building: as long as there are no deformations, the floors lie on parallel planes.
  
• Intersecting Planes
  When two planes are not parallel, they intersect. This intersection forms a line.
  

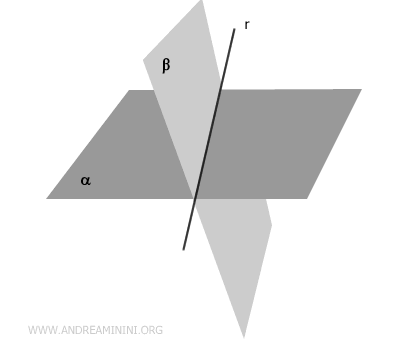
In three-dimensional space, two planes cannot intersect at a single point; their intersection, if it exists, always forms a line (proof).

The parallel relationship between planes has the following properties:

• Reflexive
  A plane is always parallel to itself.
• Symmetric
  If plane A is parallel to plane B, then plane B is parallel to plane A.
• Transitive
  If plane A is parallel to plane B, and plane B is parallel to plane C, then plane A is parallel to plane C.

The position of a line relative to a plane in three-dimensional space can be categorized as follows:

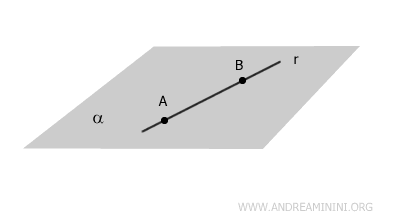
• Coplanar Line
  The line lies entirely on the plane, meaning every point on the line is also on the plane.
  
• Intersecting Line
  The line intersects the plane at a single point.
  
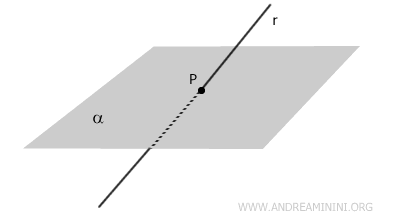
• Parallel Line
  The line has no points in common with the plane.
  

These relationships are fundamental for understanding three-dimensional geometry.

Postulates of Space

The main postulates of space in geometry include:

• Through three distinct, non-collinear points, there exists exactly one plane.
  
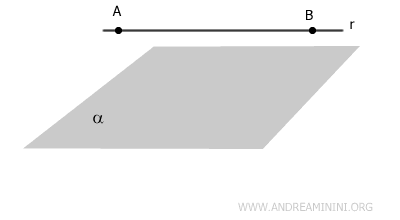
• For any two distinct points on a plane, the line passing through those points lies entirely on that plane.
  
• Partition Postulate
  A plane divides the points in space that do not lie on the plane into two regions called half-spaces. The plane itself is referred to as the origin of the half-spaces.
  
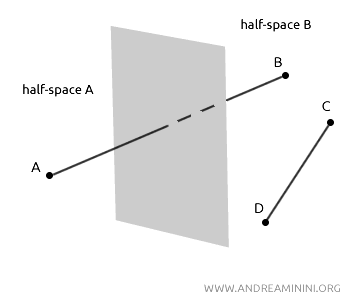
  If two points, A and B, are located in different half-spaces, the segment AB will intersect the plane. Conversely, if two points, C and D, are in the same half-space, the segment CD will not intersect the plane.

Additional Notes

Some additional insights on space in geometry:

• Space in Physics
  In physics, space is a cornerstone of relativity theory. Albert Einstein’s theory of spacetime redefined space, not as a fixed entity, but as something interdependent with time. This concept, called "spacetime," explains phenomena such as time dilation and space contraction in the presence of high speeds or strong gravitational fields. However, these considerations do not apply to geometric space.

And so on.