Dihedral Angles

A dihedral angle is a geometric figure formed by the intersection of two half-planes, known as "faces," that share a common line called an "edge."

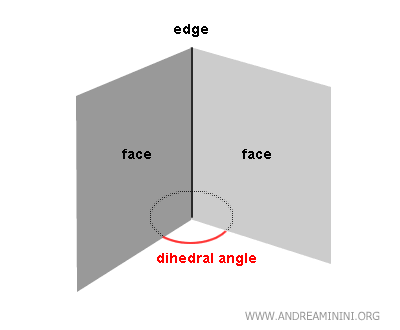
This concept is fundamental in three-dimensional geometry.

The two half-planes divide space into two distinct regions, each forming a dihedral angle.

The faces of a dihedral angle define its boundary or surface.

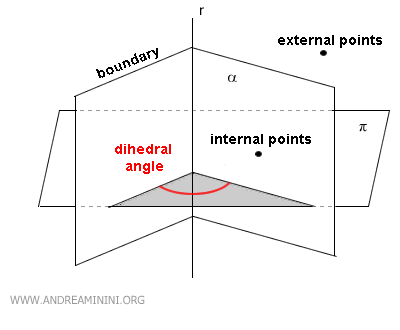
Points within the dihedral angle that do not lie on the surface are called internal points.

The angle between the two half-planes, relative to a plane π, is referred to as the dihedral angle. This angle can be either concave or convex.

If the plane π is perpendicular to the edge (r), the dihedral angle is known as the normal section of the dihedral.

The Difference Between a Dihedral and a Polyhedron: A dihedral is a space defined by two half-planes that share a line and form an angle. A polyhedron, on the other hand, is a solid figure bounded by flat surfaces called "faces." The lines where two faces meet are called "edges," and the points where three or more edges meet are called "vertices." Examples of polyhedra include cubes, pyramids, and prisms. In essence, while a dihedral is defined by two planes and an angle, a polyhedron is a three-dimensional solid with multiple flat faces.

Sections of a Dihedral

The dihedral section is the angle formed by the intersection of the dihedral and a plane that cuts through its edge.

In simple terms, the section is the projection of the dihedral angle onto a specific plane.

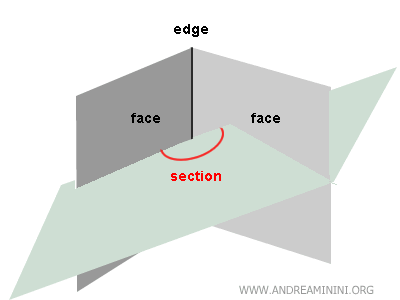
This shows that the equivalent of a dihedral in plane geometry is an angle.

Specifically, the section is called a "normal section" when the plane intersecting the dihedral is perpendicular to the edge.

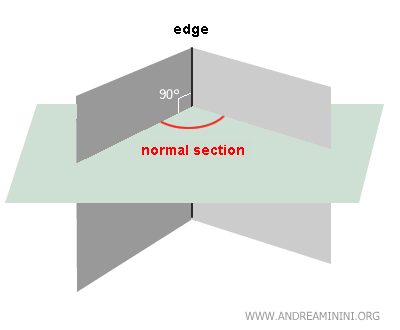
All the properties of a dihedral are derived from its normal section.

For instance, the normal section helps determine whether the dihedral is convex or concave:

• Convex Dihedral
  A convex dihedral does not contain extensions of its faces. Its normal section measures less than 180°.
• Concave Dihedral
  A concave dihedral includes extensions of its faces. Its normal section measures more than 180°.

Note: When the normal section measures exactly 180°, equivalent to a straight angle, the dihedral forms a flat plane that intersects perpendicularly with another. In this case, the section corresponds to the line created by the intersection of the two planes, and the dihedral is referred to as a flat dihedral (180°). When the faces coincide, the dihedral is called a full dihedral if it encompasses all points in space, or a null dihedral if it contains no internal points.

Depending on the angle of the section, a dihedral can also be classified as right (90°), obtuse (>90°), or acute (<90°).

• Right Dihedral
  A right dihedral has a normal section of 90°. It represents exactly half of a flat dihedral.
• Acute Dihedral
  Dihedrals with a normal section measuring less than 90° are called acute dihedrals.
• Obtuse Dihedral
  Dihedrals with a normal section measuring more than 90° but less than 180° are called obtuse dihedrals.
  

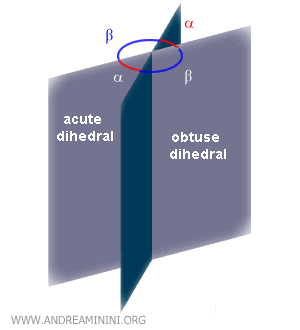
Based on their normal sections, two dihedrals can be complementary, supplementary, or explementary.

• Complementary Dihedrals
  Two dihedrals are complementary when their sum equals a right dihedral (90°).
• Supplementary Dihedrals
  Two dihedrals are supplementary when their sum equals a flat dihedral (180°).
• Explementary Dihedrals
  Two dihedrals are explementary when their sum equals a full dihedral (360°).

Example: Dihedrals α and β are supplementary because their sum equals a flat dihedral (180°).

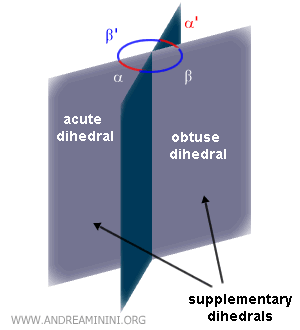
Dihedral Congruence

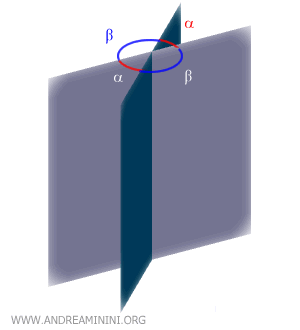
Two dihedrals are congruent when they have the same normal section.

In other words, two dihedrals are congruent if and only if they can be superimposed through rigid transformations.

In any case, congruent dihedrals have congruent normal sections.

Example: Dihedrals α and β are congruent because they share the same normal section (90°).

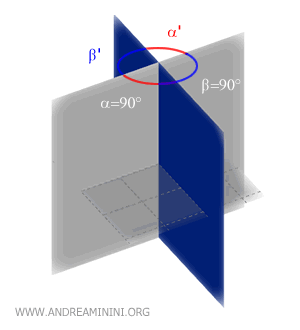
Dihedrals Opposite the Edge

Two dihedrals are referred to as opposite dihedrals if they share a common edge and the faces of one dihedral extend the faces of the other.

For example, angles α and α' are opposite angles along the edge.

Dihedrals that are opposite along the edge are always congruent.

This is similar to how vertically opposite angles are congruent in plane geometry.

Consecutive and Adjacent Dihedrals

Dihedrals can be classified as consecutive or adjacent based on their relative positions:

• Consecutive Dihedrals
  Two dihedrals are consecutive if they share the same edge and one face.
• Adjacent Dihedrals
  Two dihedrals are adjacent if they are consecutive and their non-common faces are opposite half-planes.

  Note: Two adjacent dihedrals are also supplementary because the sum of their dihedral angles equals 180°. For example, dihedrals α and β are consecutive because they share the same edge and a face. They are also adjacent because their other faces are opposite.
  
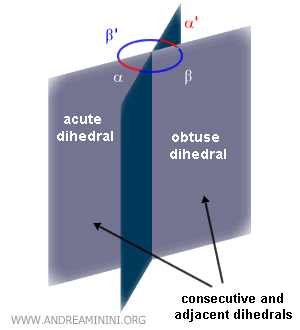
  Similarly, dihedrals α and β', α' and β', and α' and β are adjacent for the same reasons. Conversely, the pair of dihedrals α and α' are not consecutive.

Additional Notes

Here are some additional points to consider:

• Two non-parallel planes generate four dihedrals, forming two pairs of dihedrals opposite the edge.
• Two planes are perpendicular if they form four right dihedrals
  Since dihedral angles opposite the edge are congruent, it only takes one right dihedral for the others to be right as well.
  
• Two half-planes that share an edge divide space into two explementary dihedrals because their dihedral angles add up to 360°. If the two dihedrals are not flat, one will have a dihedral angle of less than 180° (convex), and the other will have a dihedral angle of more than 180° (concave).
  
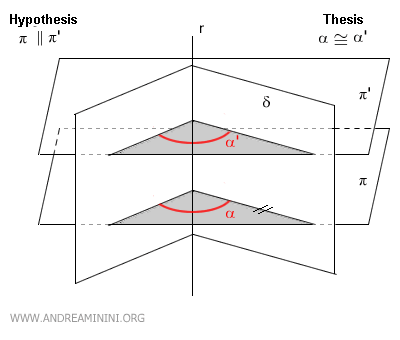
• Parallel sections of a dihedral are congruent
  The parallel sections π and π' of the dihedral δ have the same dihedral angle α≅α'.
  
• The sum of two consecutive dihedrals forms a dihedral with the same edge and non-common faces.

And so on.