Solid Angles

A solid angle is a three-dimensional geometric figure formed by taking a polygon and a point V located outside the plane of the polygon, where all rays originating from V pass through the vertices of the polygon.

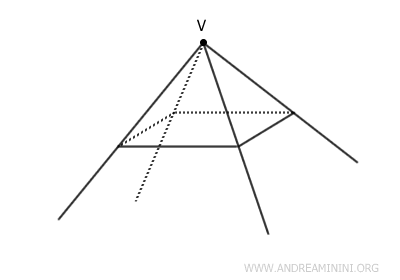
Unlike flat surfaces, a solid angle does not have a "closed" boundary, as the rays extend infinitely.

It can be thought of as a generalization of an angle in three-dimensional space.

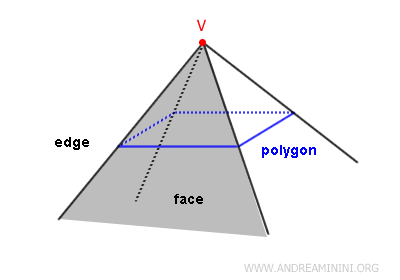
A solid angle consists of the following key components:

• Vertex (V)
  The unique origin point from which all rays defining the solid angle emanate.
• Edges
  Rays that start from the vertex V and pass through the vertices of the polygon. Each edge is defined by the ray's intersection with a vertex of the polygon.
• Faces
  The regions between two consecutive edges, with vertex V as the common point. Each face corresponds to an angle of the polygon on which the solid angle is based.

A solid angle with n edges has n faces and is referred to as an n-sided polyhedron.

For example, a trihedron is a solid angle formed by three edges and three faces.

A solid angle is considered regular if all its faces are congruent.

Note. Solid angles frequently appear in the study of projections, shadows, and optical phenomena such as light refraction.

Types of edges in a solid angle

A solid angle with a polygonal base and a single apex has two distinct types of edges:

• Lateral edges
  These edges extend from the apex of the solid angle to the vertices of the base. Each lateral edge is shared by two adjacent lateral faces.
• Base edges
  These edges belong to the polygonal base. Each base edge serves as a boundary between two lateral faces and the base itself.
  

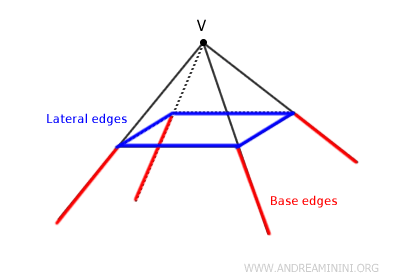
Note. When discussing the edges of a solid angle, it’s important to be mindful of notation. Some texts refer only to the lateral edges, while others include both lateral and base edges.

Key Observations

Here are some important properties of solid angles:

• The number of lateral edges in a solid angle matches the number of vertices in its base polygon
  If the base polygon has $ n $ sides, the solid angle will have $ n $ lateral edges.

  Note. If we also count the base edges along with the lateral edges, the total number of edges in a solid angle is twice the number of vertices $ n $ in the base polygon, i.e., $ 2n $

• The number of lateral faces in a solid angle equals the number of sides of its base polygon
  Each side of the base polygon generates a lateral face that extends from that side to the apex. Since a polygon with $ n $ sides has $ n $ internal angles, the solid angle will also have $ n $ lateral faces.

  Note. Including the base face, a solid angle consists of a total of $ n+1 $ faces.

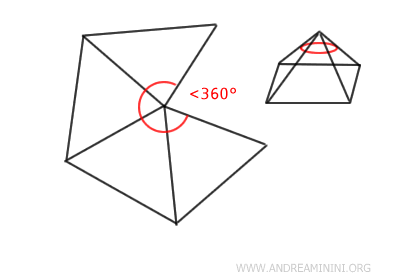
• The sum of the face angles at any vertex of a solid angle is always less than 360°
  If the sum were exactly 360°, the solid angle would collapse into a flat surface.
• Every edge in a solid angle defines a dihedral angle between two adjacent faces
  A dihedral angle is the angle formed by the intersection of two faces along a common edge. In a solid angle, each lateral edge creates a dihedral angle between the two lateral faces that share it. Each base edge, on the other hand, forms a dihedral angle between a lateral face and the base face.

  How many dihedral angles does a solid angle have? Including the base face, the total number of dihedral angles in a solid angle equals the total number of edges. If the base has $ n $ sides, there are $ 2n $ dihedral angles: $ n $ between lateral faces and $ n $ between lateral faces and the base.

• In a polyhedral angle, the sum of the angles at the vertex is less than a full rotation
  If the sum were exactly one full rotation, the vertex would lie in the same plane as the base polygon. This would mean that the vertex does not extend into three-dimensional space. In such a case, the half-planes would all lie in a single plane, eliminating any three-dimensional structure.
  
• In any polyhedral angle, each face angle is smaller than the sum of the remaining angles
  This principle is analogous to the triangle inequality, which states that in any triangle, the length of one side is always less than the sum of the other two. However, in this case, the concept extends to three dimensions and applies to the dihedral angles of a polyhedral angle rather than the sides of a triangle.

  Proof. We aim to show that in a polyhedral angle, each angle is strictly less than the sum of the others. That is, for any given angle \( \alpha_k \) in the polyhedral angle, the following inequality holds: \[ \alpha_k < \sum_{j \neq k} \alpha_j \] In other words, given a polyhedral angle with vertex angles \( \alpha_1, \alpha_2, ..., \alpha_n \), we must show that for every choice of \( k \): \[ \alpha_k < \alpha_1 + \alpha_2 + ... + \alpha_{k-1} + \alpha_{k+1} + ... + \alpha_n \] A key property of polyhedral angles is that their total angle sum is always less than 360°: \[ \alpha_1 + \alpha_2 + \dots + \alpha_n < 360^\circ \] This serves as the foundation for our proof. Now, isolating an arbitrary angle \( \alpha_k \) within this sum: \[ \alpha_k + (\alpha_1 + \alpha_2 + \dots + \alpha_{k-1} + \alpha_{k+1} + \dots + \alpha_n) < 360^\circ \] Defining the sum of the remaining angles (excluding \( \alpha_k \)) as \( S \): \[ S = \alpha_1 + \alpha_2 + \dots + \alpha_{k-1} + \alpha_{k+1} + \dots + \alpha_n \] we can rewrite the inequality as: \[ \alpha_k + S < 360^\circ \] Since we already established that the total angle sum is less than 360°, it follows that \( S \) (which excludes \( \alpha_k \)) must also be less than 360°: \[ S < 360^\circ \] We now seek to show that: \[ S > \alpha_k \] where \( S \) represents the sum of all angles except \( \alpha_k \). Subtracting \( \alpha_k \) from both sides of our previous inequality: \[ \alpha_k + S < 360^\circ \] \[ S < 360^\circ - \alpha_k \] Since \( S \) is already known to be less than 360°, the only way for this inequality to hold is if \( \alpha_k < S \). $$ \alpha_k < S $$ Substituting \( S \) back in: \[ \alpha_k < \alpha_1 + \alpha_2 + \dots + \alpha_{k-1} + \alpha_{k+1} + \dots + \alpha_n \] \[ \alpha_k < \sum_{j \neq k} \alpha_j \] This confirms that in any polyhedral angle, each individual angle is strictly less than the sum of the remaining angles. The result follows directly from the fact that the total angle sum is less than 360° and that all individual angles are positive.

• In a trihedral angle, each face angle is greater than the absolute difference of the other two
  This property is a direct consequence of the sum constraint in a polyhedral angle.

  Proof. A trihedral angle is a three-dimensional geometric figure formed by three half-planes intersecting along three half-lines, all sharing a common vertex. If we denote the dihedral angles between the faces as \( \alpha, \beta, \gamma \), we already know that their sum is always less than 360°: \[ \alpha + \beta + \gamma < 360^\circ \] Mathematically, we aim to prove that for each angle \( \alpha, \beta, \gamma \), the following inequalities hold: \[ \alpha > |\beta - \gamma| \] \[ \beta > |\alpha - \gamma| \] \[ \gamma > |\alpha - \beta| \] This follows from reasoning similar to the triangle inequality but applied to dihedral angles. Since we know that: \[ \alpha + \beta + \gamma < 360^\circ \] we can conclude that each angle is smaller than the sum of the other two: \[ \alpha < \beta + \gamma \] \[ \beta < \alpha + \gamma \] \[ \gamma < \alpha + \beta \] These inequalities are fundamental and stem directly from the properties of polyhedral angles. Now, consider the absolute difference between two angles. Take \( \alpha \) and \( \beta \), with \( \gamma \) being the third angle: \[ \alpha > | \beta - \gamma | \quad \text{if and only if} \quad \alpha + \gamma > \beta \] This holds because we have already established that \( \beta < \alpha + \gamma \). By similar reasoning, we obtain: \[ \beta > | \alpha - \gamma | \] \[ \gamma > | \alpha - \beta | \] The absolute value is necessary because if \( \beta > \gamma \), then \( \beta - \gamma \) is positive, whereas if \( \beta < \gamma \), the difference is negative, and we must consider its absolute value. This proves that in a trihedral angle, each dihedral angle is always greater than the absolute difference of the other two.

And so on.