Cylinder
A cylinder is a solid formed by rotating a rectangle completely around a line (called the "axis") that passes through one of its sides.
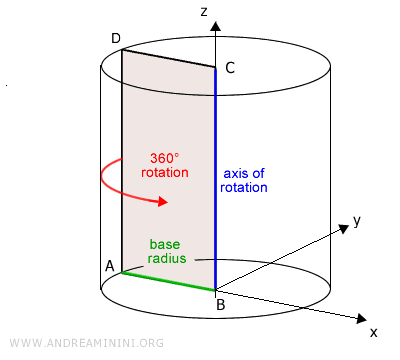
Therefore, a cylinder is a type of solid of rotation.
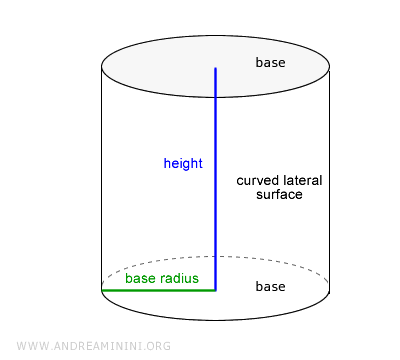
The distance from the axis to the opposite side of the rectangle is called the "base radius" or "cylinder radius."
The cylinder is bounded by two circular surfaces known as "bases" and a curved lateral surface.
The height of the cylinder is the distance between the two bases. It is the side around which the cylinder rotates and is perpendicular to the bases.
When the height of a cylinder equals the diameter of the base, it is called an equilateral cylinder.
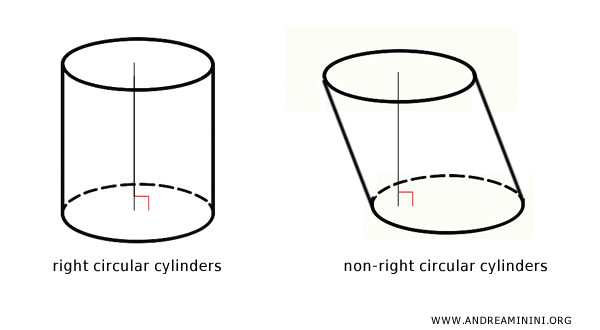
Note: In elementary geometry, the term "cylinder" typically refers to a "right circular cylinder." There are, however, other types of cylinders, known as "indefinite cylinders," such as the elliptical cylinder, parabolic cylinder, hyperbolic cylinder, and various forms of non-right circular cylinders (e.g., oblique cylinders). Unlike the right circular cylinder, these shapes can't be generated by simply rotating a rectangle around one of its sides. In such cases, the cylinder’s height does not coincide with the axis of rotation.
Formulas
Here are some key formulas for calculating properties of a right circular cylinder:
- Base Area
The area of the cylinder's base is calculated like the area of a circle: $$ S_B = \pi r^2 $$ - Lateral Surface Area
The area of the cylinder's lateral surface is found by multiplying the circumference of the base by the height of the cylinder. For a right circular cylinder, the formula is:
$$ S_L = 2 \pi r \cdot h $$ where r is the base radius, and π is the constant pi (approximately 3.14159). - Total Surface Area
The total surface area is the sum of the lateral area and the area of the two bases. Since the bases of a right circular cylinder are circles, the area of each base is πr2. Thus, the formula for the total area is:
$$ S_T = S_L + 2 \cdot \pi r^2 $$ $$ S_T = 2 \pi r \cdot h + 2 \cdot \pi r^2 $$ $$ S_T = 2 \pi r \cdot (h + r) $$Explanation. To make the formula more intuitive, let’s visualize the cylinder as if it were unrolled onto a flat surface.
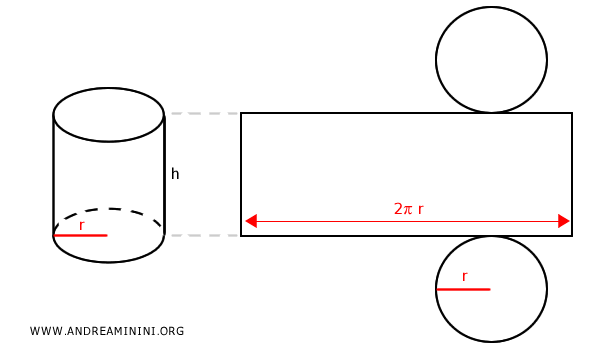
When unwrapped, the lateral surface of the cylinder forms a rectangle. The width of this rectangle corresponds to the circumference of the base (2πr), while the height remains the same as the height of the cylinder (h). $$ S_L = 2 \pi r \cdot h $$ The area of each base is simply the area of a circle: $$ S_B = \pi r^2 $$ Therefore, the total surface area of the cylinder is the sum of the areas of the two circular bases and the lateral surface: $$ S_T = 2 S_B + S_L $$ $$ S_T = 2 ( \pi r^2 ) + 2 \pi r \cdot h $$ $$ S_T = 2 \pi r^2 + 2 \pi r h $$ $$ S_T = 2 \pi r \cdot ( r + h ) $$ Which is precisely the formula we set out to derive. - Volume
The volume V of a right circular cylinder is calculated by multiplying the base area by the height h of the cylinder. For a circular base with radius r, the base area is πr2. Therefore, the volume of the cylinder is given by: $$ V = \pi r^2 \cdot h $$ This formula applies to any right circular cylinder, regardless of whether it is oblique, as the volume depends only on the base area and the perpendicular height.Note. By the volume equivalence theorem for cylinders and prisms, the volume can be expressed as $$ V = A \cdot h = \pi r^2 h $$
Types of Cylinders
There are several types of cylinders:
- Right Circular Cylinder
It has circular bases with the lateral surface perpendicular to the bases. - Non-Right Circular Cylinder
This type also has circular bases, but the lateral surface is not perpendicular to the bases. It can be tilted (oblique cylinder) or feature curves or twists. - Oblique Cylinder
If the generating lines are tilted relative to the bases, the cylinder is oblique. In this case, the cross-section is not a rectangle. - Elliptical Cylinder
This cylinder has elliptical bases instead of circular ones. - Parabolic Cylinder
This cylinder has no fixed bases and extends infinitely in one direction, with a cross-section that forms a parabola. - Hyperbolic Cylinder
Similar to the parabolic cylinder, but with a cross-section that forms a hyperbola.
These are just a few examples of "indefinite" or non-right cylinders. Many other cylindrical shapes are possible, depending on the curves of the bases and the nature of the lateral surfaces.
The Cylinder in Analytical Geometry
The concept of a cylinder also extends into analytical geometry, where it can be represented using equations in Cartesian, cylindrical, or spherical coordinates.
A right circular cylinder with its axis along the z-axis and the center of the base at the origin has the equation:
$$ x^2 + y^2 = r^2 $$
Where r is the radius of the circular bases.
This equation describes all points (x, y, z) whose distance from the z-axis is consistently equal to r.
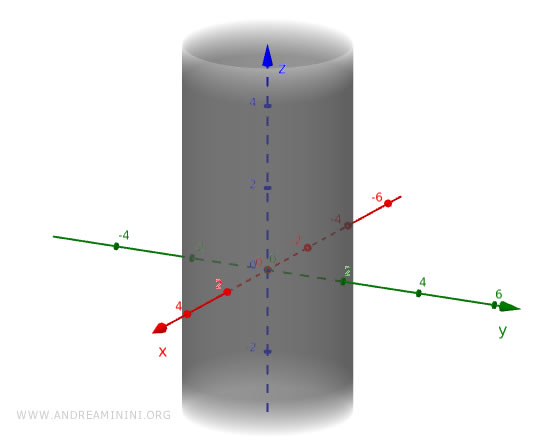
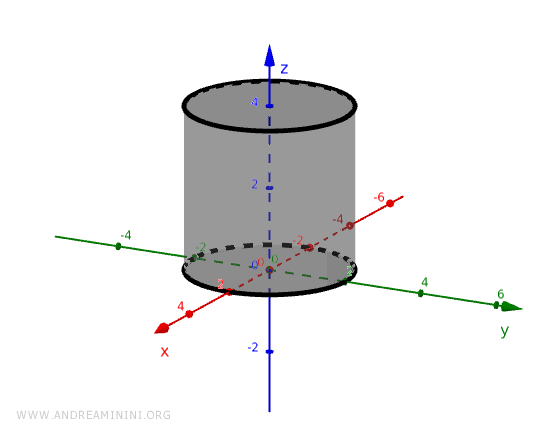
Since this surface extends infinitely, to define a finite cylinder, we must also specify an interval for the z-axis values.
For example, if the cylinder extends from the origin (0,0,0) upwards to a height h, the interval for z is:
$$ 0 \le z \le h $$
The result is a cylinder with a finite height and a base on the xy-plane.
Circular Cylinder
The equation of an infinite circular cylinder is given by $$ x^2 + y^2 + a x + b y + c = 0 $$
This equation defines a circular cylindrical surface if and only if the directrix curve in the $xy$-plane is indeed a circle. This happens precisely when the following condition is met:
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
The term “infinite” indicates that the cylinder has no finite height; it extends infinitely in both directions along its axis of generators.
Proof. Let’s begin with the equation $$ x^2 + a x + y^2 + b y + c = 0 $$ Group the $x$ and $y$ terms: $$ (x^2 + a x) + (y^2 + b y) + c = 0 $$ Next, complete the square by adding and subtracting $ \frac{a^2}{2^2} $ and $ \frac{b^2}{2^2} $: $$ (x^2 + a x + \frac{a^2}{2^2} - \frac{a^2}{2^2}) + (y^2 + b y + \frac{b^2}{2^2} - \frac{b^2}{2^2}) + c = 0 $$ $$ (x^2 + a x + \frac{a^2}{2^2}) + (y^2 + b y + \frac{b^2}{2^2}) + c - \frac{a^2}{2^2} - \frac{b^2}{2^2} = 0 $$ $$ (x^2 + a x + \left(\frac{a}{2}\right)^2) + (y^2 + b y + \left(\frac{b}{2}\right)^2) = \frac{a^2}{2^2} + \frac{b^2}{2^2} - c $$ Completing the squares gives: $$ \left( x + \frac{a}{2} \right)^2 + \left( y + \frac{b}{2} \right)^2 = \frac{a^2}{4} + \frac{b^2}{4} - c $$ For this to represent a real circle (i.e. with a real, non-imaginary radius), the right-hand side must be non-negative: $$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
The same reasoning extends to other coordinate planes:
- In the xz-plane, the equation in $x$ and $z$ is $$ x^2 + z^2 + a x + b z + c = 0 $$ In this case, the cylinder is circular with its axis parallel to $y$.
- In the yz-plane, the equation in $y$ and $z$ is $$ y^2 + z^2 + a y + b z + c = 0 $$ Here, the cylinder is circular with its axis parallel to $x$.
Example
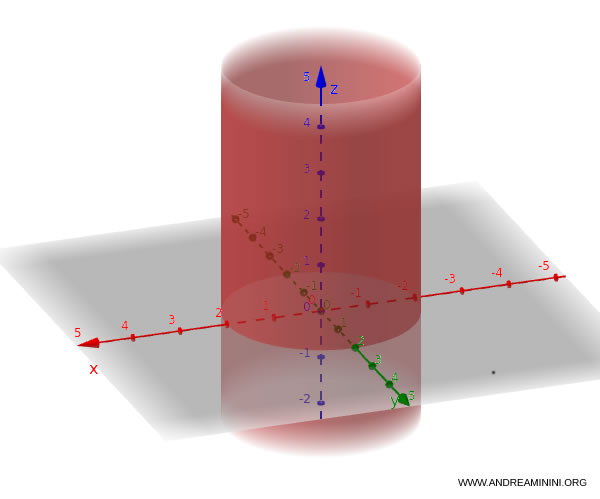
Here’s an example of an infinite circular cylinder:
$$ \frac{x^2}{4} + \frac{y^2}{4} = 1 $$
This equation describes a circular cylindrical surface.
Hyperbolic Cylinder
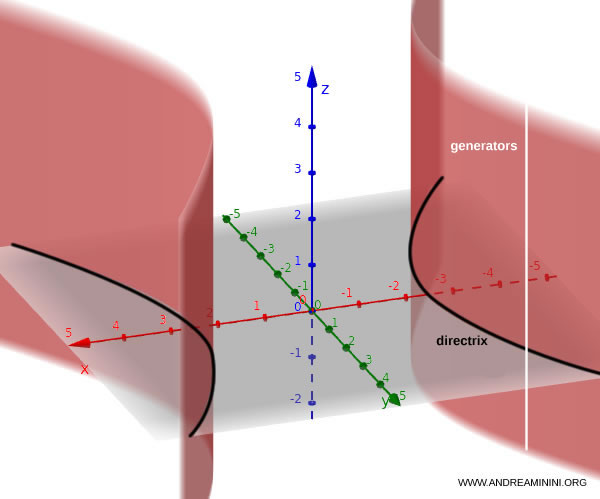
A hyperbolic cylinder is a three-dimensional surface generated by translating a single hyperbola along a direction parallel to one of the coordinate axes. Its general equation is: $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$ This expression defines a surface that extends infinitely for all values of $z$.
Put simply, no matter what the $z$-coordinate is, the points $(x, y)$ always lie on the same hyperbola in the $xy$-plane.
The surface of a hyperbolic cylinder is characterized by two fundamental elements:
- Directrix: this is the hyperbola defined in the $xy$-plane by the equation $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$. The curve has two open branches extending outward, separated by its asymptotes.
- Generators: these are straight lines running parallel to the $z$-axis. Sliding the hyperbola along these lines sweeps out the three-dimensional surface of the hyperbolic cylinder.
In essence, a hyperbolic cylinder is a ruled surface because it’s composed of infinitely many straight-line generators, and it’s considered a cylindrical surface because its cross-section in planes parallel to the $xy$-plane always yields the same hyperbola.
The axis along which the generators run determines the orientation of the cylinder. In the equation $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$, this axis is parallel to the $z$-axis.
If you replace the $z$-axis with either the $x$-axis or the $y$-axis, the orientation of the hyperbolic cylinder changes accordingly.
Example. Let’s examine the equation: $$ \frac{x^2}{2} - \frac{y^2}{4} = 3 $$ In this case, the directrix lies in the $xy$-plane, and the hyperbola opens along the $x$-axis. The equation of the directrix can be rewritten as: $$ x^2 = 2 \left( 3 + \frac{y^2}{4} \right ) $$ or equivalently: $$ y^2 = 4 \left( \frac{x^2}{2} - 3 \right ) $$ The generators are lines parallel to the $z$-axis. This means that for every point $(x, y)$ on the hyperbola, there’s a vertical line extending indefinitely along the $z$-direction.
Parabolic Cylinder
A parabolic cylinder is a three-dimensional surface created by translating a parabola along a direction parallel to one of the Cartesian axes. Its general equation is: $$ y = k x^2 $$ where $k$ is a real constant. In this case, the axis of the parabolic cylinder runs parallel to the $z$-axis.
When this relationship holds for all values of $z$, the surface extends infinitely along the $z$-axis. Such a cylinder is called "infinite" because it doesn’t have a fixed height.
Example. Let’s take the directrix $ y = x^2 $, which is a parabola. The corresponding surface can be described by the equation $$y = x^2, \quad z \in \mathbb{R} $$ This surface consists of infinitely many identical parabolas lying in the $x\text{-}y$ plane and repeated along the $z$-axis.
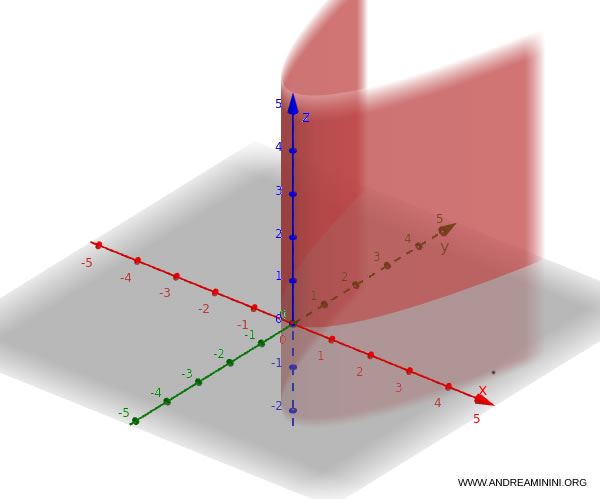
It’s essentially like placing a parabola in the $xy$ plane and sliding it upward and downward along a direction parallel to the $z$-axis.
If the parabola lies instead in the $x\text{-}z$ plane, the equation becomes:
$$ z = x^2 $$
In this case, the axis of the parabolic cylinder is parallel to the $y$-axis, since $y$ is free to take on any value.
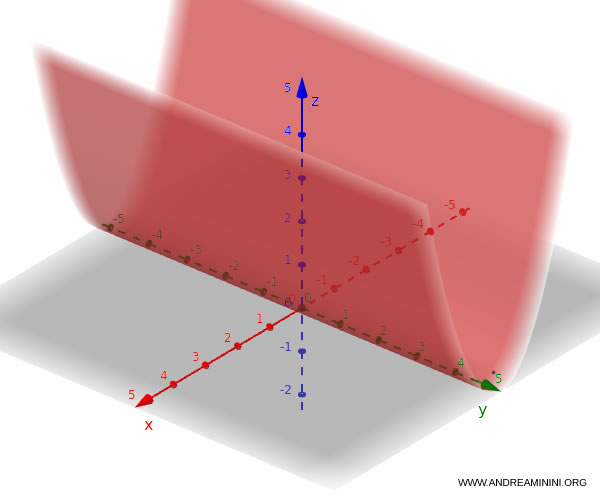
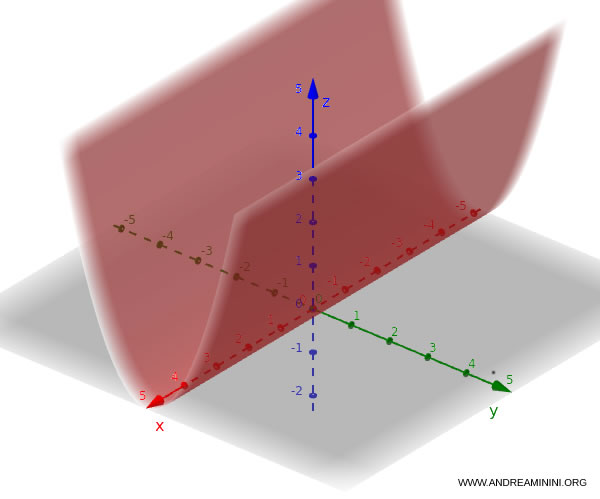
Similarly, if the parabola lies in the $y\text{-}z$ plane, the equation is:
$$ z = y^2 $$
In this case, the axis of the parabolic cylinder runs parallel to the $x$-axis.
Observations
Here are some additional notes and observations about cylinders:
- Two right circular cylinders are congruent if they have the same height and base radius.
- If you cut a right circular cylinder with a plane that passes through the axis of rotation and is perpendicular to the base, you get a rectangle, or a square if the cylinder is also equilateral.
- The cylinder is similar to a prism with a polygonal base, but since it has circular bases, it possesses unique properties, such as rotational symmetry around its axis.
- Volume Equivalence Between a Prism and a Cylinder
A prism and a cylinder - regardless of the shape of the base - have the same volume if they share the same base area $A$ and height $h$.
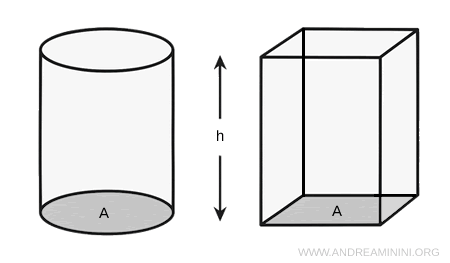
Proof. In both cases, the volume is calculated using the same formula: $$ V = A \cdot h $$ where $A$ is the area of the base and $h$ is the height (i.e., the perpendicular distance between the two bases).
And so on...
