Pyramids
A pyramid is a polyhedron formed when a solid angle is intersected by a plane that cuts through all its edges. The resulting cross-section is known as the pyramid’s base, which can take various polygonal shapes. The vertex of the solid angle becomes the pyramid’s vertex.
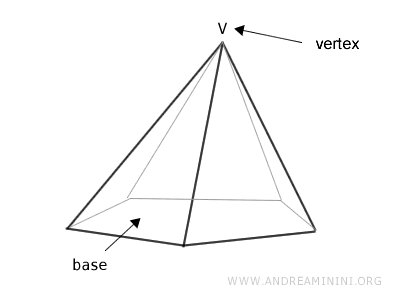
The base of the pyramid is a polygon, while the lateral faces are triangles.
The edges that outline the base are called base edges, while the edges connecting the base to the vertex are known as lateral edges.
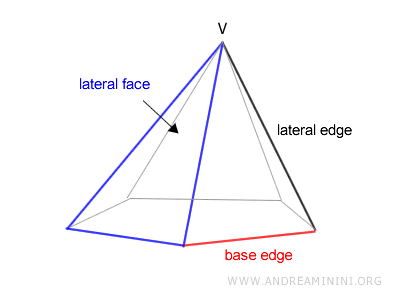
A key feature of a pyramid is its height, which is the perpendicular distance from the vertex to the plane of the base.
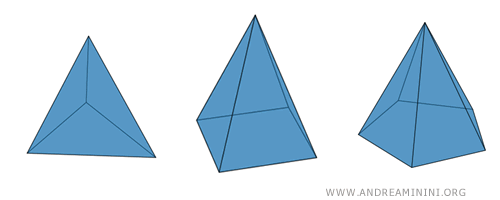
Depending on the number of sides of the base, a pyramid can be triangular, quadrilateral, pentagonal, and so on.
In any pyramid, the number of vertices matches the number of faces, including the base. Moreover, a pyramid must have at least four faces. The pyramid with the fewest faces is the tetrahedron, consisting of four triangular faces.
Types of Pyramids
There are different types of pyramids:
- Pyramids with Triangular or Square Bases
A pyramid’s base can be a triangle, a quadrilateral, or any other polygon, whether regular or irregular. If the base is a triangle, the pyramid is classified as a triangular pyramid. When the base is a square, it is specifically called a square-based pyramid. More generally, if the base is any type of quadrilateral, it is referred to as a quadrangular pyramid. The classification extends to pyramids with bases of other polygonal shapes accordingly.
- Right Pyramid
A pyramid is called a right pyramid when its base ABCD can be inscribed in a circle, and the vertex (V) is directly above the center (O) of the circumcircle of the base.
In other words, the vertex of the pyramid is the orthogonal projection of the center of the base's circumcircle. In right pyramids, the height of the pyramid is perpendicular to the center (O) of the base (segment OV). The heights of the lateral faces in a right pyramid are called apothems.
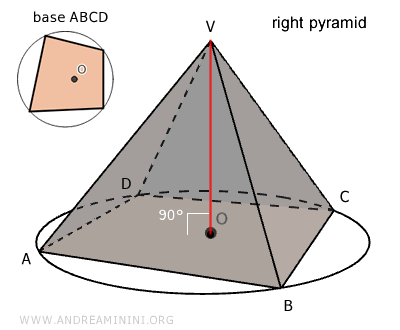
Alternatively, a pyramid can also be considered right if a circle can be inscribed within its base, with its center O serving as the orthogonal projection of the pyramid’s apex V onto the plane of the base.
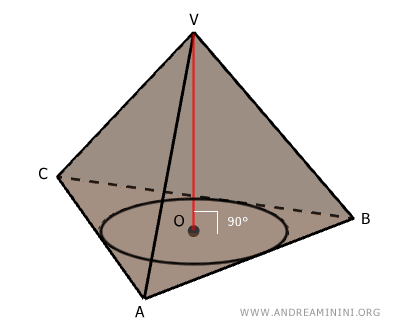
Any pyramid that is not a right pyramid is called an oblique pyramid.
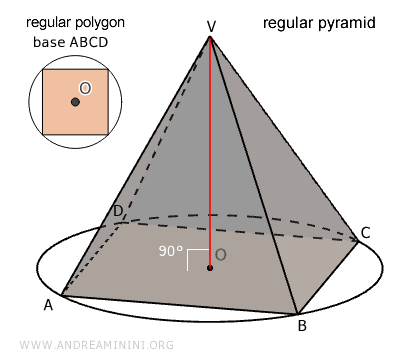
- Regular Pyramid
A regular pyramid is a right pyramid whose base ABCD is a regular polygon.
Since the base is a regular polygon, it can always be inscribed in and circumscribed by a circle. As a result, all the lateral faces of the pyramid are congruent isosceles triangles with equal heights (apothems). Additionally, because it is a right pyramid, the height of the pyramid intersects the center (O) of the base (segment OV).
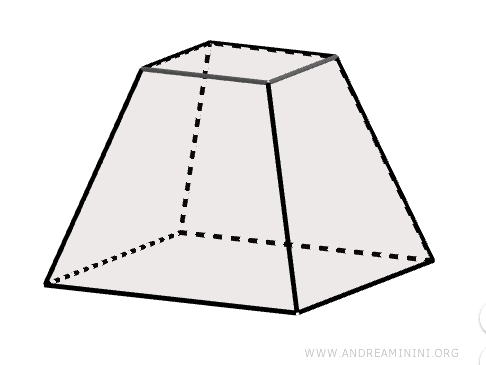
- Pyramid Frustum
A pyramid frustum is a solid figure obtained by slicing a pyramid with a plane parallel to its base.
Theorem of the Apothem in a Right Pyramid
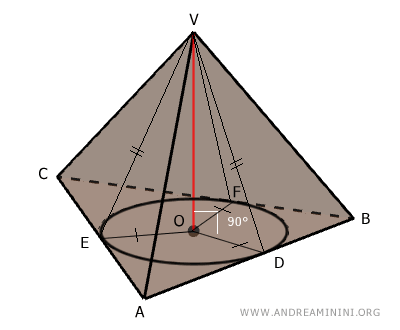
In a right pyramid, the heights of the lateral faces (apothems) are congruent, so VD ≅ VE ≅ VF, and they pass through the points of tangency D, E, F where the base edges touch the inscribed circle.
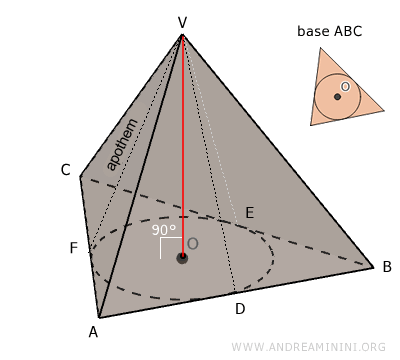
In the previous example, the apothems are the segments VD, VE, and VF, and they are congruent.
$$ \overline{VD} \cong \overline{VE} \cong \overline{VF} $$
This result is useful in determining the metric properties of pyramids.
Formulas
The Volume of a Pyramid
The volume \( V \) of a pyramid is given by the formula:
$$ V = \frac{1}{3} \cdot (\text{area of the base}) \cdot (\text{height}) $$
This formula applies regardless of the shape of the base.
Thus, calculating the volume of a pyramid is quite simple as long as the area of the base and the height of the pyramid are known.
Note: The volume of a pyramid is one-third of the product of the area of the base and the height because any pyramid is equivalent to one-third of a prism with the same base and height. See equivalent solids.
Lateral Surface Area
The lateral surface area of a pyramid is the sum of the areas of its lateral faces.
In the case of a regular pyramid, the lateral surface area equals the semiperimeter (p) of the base multiplied by the apothem (a).
$$ A_L = p \cdot a $$
Total Surface Area
The total surface area of a pyramid is the sum of the areas of all its faces, including the base.
$$ A = A_L + A_B $$
Where AL is the lateral surface area, and AB is the area of the base.
Example. For a right pyramid with a square base, its net consists of one square (the base) and four identical isosceles triangles, each with a height equal to the slant height (a).
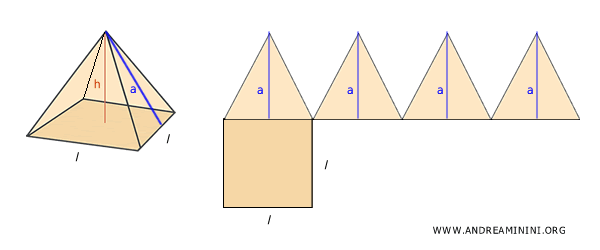
The lateral surface area of the pyramid is given by the sum of the areas of the four triangular faces: $$ A_l = \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a $$ which simplifies to:$$ A_l = 4 \cdot \frac{1}{2} l \cdot a $$ Since the perimeter of the base is $ P = 4l $, we can rewrite the expression as: $$ A_l = \frac{1}{2} P \cdot a $$ And using the semiperimeter $ p = \frac{1}{2} P $, we get: $$ A_l = p \cdot a $$ In other words, the lateral surface area is equal to the semiperimeter multiplied by the slant height. The total surface area is simply the sum of the lateral area and the area of the base: $$ A_t = A_b + A_l = A_b + p \cdot a $$
Additional Notes
Here are a few additional notes on pyramids:
- Pyramid Frustum
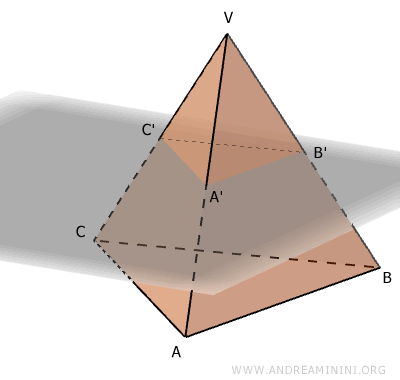
A plane parallel to the base that intersects the pyramid at a height h divides it into two parts: the upper part remains a pyramid A'B'C'V, while the lower part becomes a frustum of height h.
- Theorem of the Heights of the Lateral Faces of a Right Pyramid
In a right pyramid, the altitudes (apothems) of the lateral faces are all congruent and intersect the base at the points where the inscribed circle is tangent to its sides.
- Volume-Equivalent Pyramids
Two pyramids with equal base areas and identical heights have the same volume. Put simply, if two pyramids share the same base area $ A_b $ and height $ h $, then their volumes are equal - regardless of the shape of their bases or the orientation of their sides.
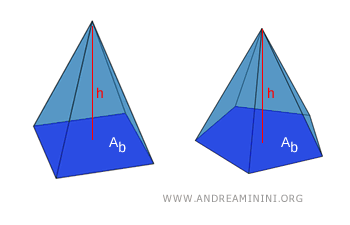
Proof. This result follows directly from the formula for the volume of a pyramid: $$ V = \frac{1}{3} \cdot \text{base area} \cdot \text{height} $$ Since the volume depends solely on the area of the base and the vertical height, any two pyramids with matching values for these parameters must have the same volume.
- A pyramid has exactly one third the volume of a prism with the same base and height
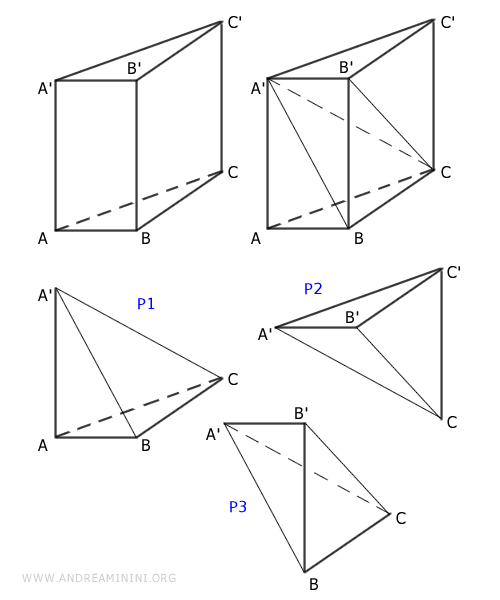
When a pyramid and a prism share congruent bases and equal heights, the pyramid’s volume is exactly one third that of the prism.Example. A triangular prism with base ABC can be decomposed into three pyramids of equal volume: P1, P2, and P3.
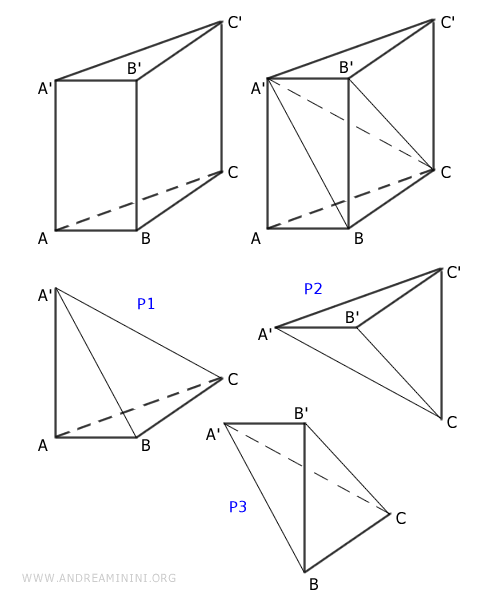
Pyramids P1 and P2 have congruent bases, $ ABC \cong A'B'C' $, and equal heights, $ AA' \cong CC' $, so they are equal in volume: $$ P1 \doteq P2 $$ Likewise, pyramids P2 and P3 share congruent bases, $ BCC' \cong BCB' $, and a common height, $ A'B' $, making them volume-equivalent as well: $$ P2 \doteq P3 $$ By transitivity, P1 and P3 must also be equal in volume: $$ P1 \doteq P2 \doteq P3 \Rightarrow P1 \doteq P3 $$ Therefore, the three pyramids formed from the prism each occupy exactly one third of its total volume. The volume of a pyramid is given by the formula: \[ V = \frac{1}{3} \cdot \text{base} \cdot \text{height} \] while the volume of a prism is: \[ V = \text{base} \cdot \text{height} \] So, when both solids share the same base area and height, the volume of the pyramid is exactly one third that of the corresponding prism. - Volume Equivalence Between a Pyramid and a Cone
A pyramid and a cone with bases of equal area and the same height have the same volume. In other words, if a pyramid and a cone share the same base area and height, then their volumes are identical. This is because the volume formula for both solids is essentially the same: $$ V = \frac{1}{3} \cdot \text{base area} \cdot \text{height} $$ So, when the base and height are the same, the volume is as well.Proof. Consider a pyramid and a cone resting on the same plane $ \alpha $, with equal base area ($ S = S' $) and the same height ($ AB \cong CD $).

To compare the two solids, let's take another plane $ \alpha' $ parallel to the base ($ \alpha' \parallel \alpha $), which cuts both the pyramid and the cone, creating cross-sections parallel to their bases. Let $ S_p $ be the area of the pyramid’s cross-section, and $ S_c $ the area of the cone’s cross-section.

From the properties of solids with polygonal and circular bases (like a frustum of a pyramid or a frustum of a cone), we know that when a solid is sliced by a plane parallel to its base, the ratio between the base area $ S $ and the cross-sectional area $ S_p $ is the square of the similarity ratio: $$ \frac{S}{S_p} = \left( \frac{AB}{A'B} \right)^2 \quad \text{(pyramid)} $$ $$ \frac{S'}{S_c} = \left( \frac{CD}{C'D} \right)^2 \quad \text{(cone)} $$ But since $ AB = CD $ and $ S = S' $ by assumption, we have: $$ \frac{S}{S_c} = \left( \frac{AB}{C'D} \right)^2 \quad \text{(cone)} $$ And because $ A'B = C'D $, the similarity ratios are the same: $$ \frac{S}{S_c} = \left( \frac{AB}{A'B} \right)^2 \quad \text{(cone)} $$ Therefore, the two cross-sections $ S_p $ and $ S_c $ have the same area: $$ \frac{S}{S_p} = \frac{S}{S_c} \quad \Rightarrow \quad S_p = S_c $$ This holds for any plane parallel to the base - that is, every horizontal cross-section of the pyramid and the cone has the same area. Since all horizontal sections are equal in both solids, by Cavalieri’s principle, the pyramid and the cone must have the same volume.
And so on.
