Regular Pyramid

A regular pyramid is a right pyramid whose base is a regular polygon, meaning all its sides and angles are equal.

In other words, the base can be an equilateral triangle, a square, a regular pentagon, or any other regular polygon.

A regular pyramid is characterized by the following properties:

• Regular base. The base is always a regular polygon, which means it can be both inscribed in and circumscribed around a circle.
• Congruent lateral faces. All lateral faces are identical isosceles triangles.
• Height. Since this is a right pyramid, its height (OV) extends perpendicularly from the base’s center, denoted as O. This point O also serves as the center of both the inscribed and circumscribed circles.
• Apothem. Each lateral face has a unique height known as the apothem, which is the perpendicular distance from the pyramid’s apex to the midpoint of a base edge. In a right pyramid, all apothems are congruent.

The regular pyramid is one of the most striking geometric forms, admired throughout history for its symmetry and structural elegance.

Note. Regular pyramids have been extensively used in architecture and engineering. The most iconic example is the Great Pyramid of Cheops in Egypt, which is based on an almost perfectly regular design.

Example of a Regular Pyramid

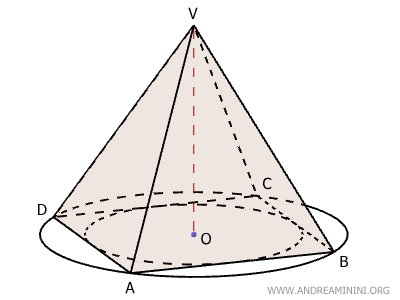
Let’s examine a pyramid with a square base (ABCD), making it a regular quadrilateral.

The apex V is positioned directly above the base’s center O. The segment OV represents the pyramid’s height and is perpendicular to the plane of the base ABCD.

The four lateral faces are congruent isosceles triangles:

$$ ABV \cong ADB \cong BCV \cong CDV $$

The height of each lateral face is known as the apothem, and it is identical across all faces. For instance, $ EV \cong FV $.

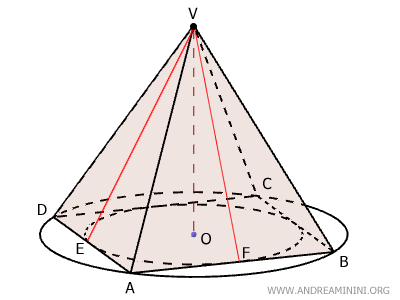
Due to its perfect symmetry, the base of the pyramid can be both inscribed in and circumscribed around a circle.

Proof

A regular pyramid has a base that is a regular polygon.

Any regular polygon can be both inscribed in and circumscribed around a circle.

Let’s focus on the points of tangency (E and F) where the inner circle touches the sides of the polygon.

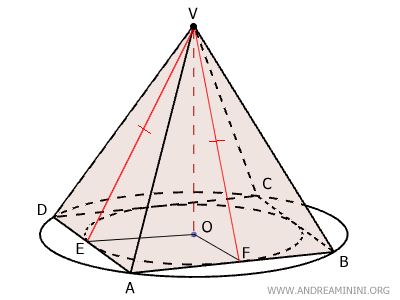
The segments EV and FV represent the apothems of the lateral faces ADV and ABV of the right pyramid (see proof). Since they are the heights of these triangular faces, they form a 90° angle with the base edges AD and AB.

The segments OE and OF are congruent because they are radii of the same circle.

$$ OE \cong OF $$

The angles $ E \hat{O} V \cong F \hat{O} V $ are both 90° because $ OV $, the height of the pyramid, is perpendicular to the base ABCD.

$$ E \hat{O} V \cong F \hat{O} V = 90° $$

By the first triangle congruence theorem, triangles OEV and OFV are congruent, as they share two congruent sides and the included right angle.

From this, it follows that $ EV \cong FV $, meaning the apothems of the pyramid are congruent.

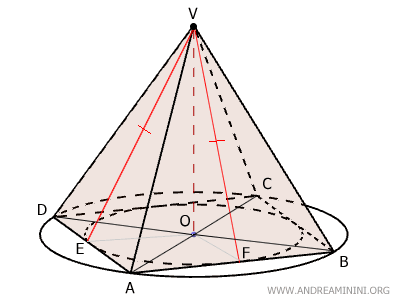
Since this reasoning applies to all lateral faces, we can conclude that in a regular pyramid, all apothems are congruent.

Now, let’s examine the segments $ OA \cong OB \cong OC \cong OD $, which are congruent because they are radii of the circumscribed circle.

The triangles $ OAV \cong OBV \cong OCV \cong ODV $ are congruent because they share two congruent sides and a right angle.

Consequently, the segments $ AV \cong BV \cong CV \cong DV $ must also be congruent.

This implies that triangles $ ABV $ and $ ADV $ are isosceles triangles, as they have two equal sides.

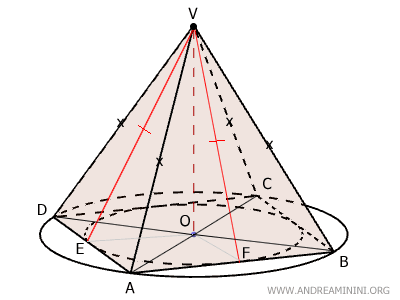
Since the height (apothema) of these isosceles triangles also serves as their median, points E and F are the midpoints of AD and AB, respectively.

$$ AE \cong ED \cong AF \cong BF $$

By the third triangle congruence theorem, triangles $ ABV \cong ADV $ are congruent because their corresponding sides are congruent.

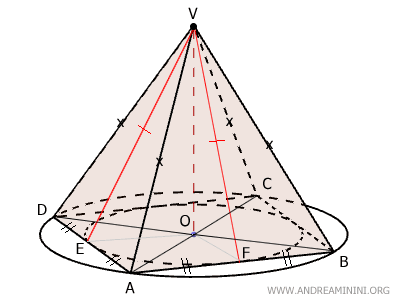
Since this argument holds for every lateral face, we can conclude that all lateral faces of a regular pyramid are congruent isosceles triangles.

Key Formulas

Below are some essential formulas for calculating the fundamental properties of a regular pyramid.

• Base Area
  The base area depends on both the number of sides and the length of each side. It can be determined using the formula: \[ A_b = \frac{n \cdot l^2}{4} \cdot \cot \frac{180^\circ}{n} \] where \( n \) is the number of sides in the base, \( l \) is the length of a single side, and \( \cot \) represents the cotangent of the central angle associated with the regular polygon. In the special case of a square base, the formula simplifies to **\( A_b = l^2 \)**, as the area of a square is straightforward to compute.

  Example. If the base is a regular pentagon with \( l = 5 \) cm, its area is given by: \[ A_b = \frac{5 \cdot 5^2}{4} \cdot \cot \frac{180^\circ}{5} \approx 43.01 \text{ cm}^2 \]

• Lateral Surface Area
  The lateral surface area accounts for the sum of all triangular faces forming the sides of the pyramid. It is calculated as: \[ A_L = \frac{n \cdot l \cdot a}{2} \] where \( n \) is the number of sides in the base, \( l \) is the side length, and \( a \) is the slant height (the apothem of the pyramid), which corresponds to the altitude of each isosceles triangular face. Since each lateral face is an isosceles triangle, its area is given by \( \frac{l \cdot a}{2} \). Multiplying by \( n \) (the number of faces) yields the total lateral surface area.

  Example. If the pyramid has a hexagonal base (\( n = 6 \)), with each side measuring \( 4 \) cm and a slant height of \( 7 \) cm, the lateral surface area is: \[ A_L = \frac{6 \cdot 4 \cdot 7}{2} = 84 \text{ cm}^2 \]

• Volume of the Pyramid
  The volume of a regular pyramid is given by the formula: \[ V = \frac{A_b \cdot h}{3} \] where \( A_b \) represents the base area and \( h \) is the vertical height of the pyramid (the perpendicular distance from the apex to the center of the base). This formula closely resembles the volume calculation for a prism, with the key difference that a pyramid occupies only one-third of the volume of a prism with the same base and height. This is due to the fact that the pyramid tapers toward its apex, reducing its overall volume compared to a solid with a uniform cross-section.

  Example. If a pyramid has a square base with a side length of \( l = 6 \) cm, meaning \( A_b = 36 \) cm², and a height of \( 10 \) cm, its volume is: \[ V = \frac{36 \cdot 10}{3} = 120 \text{ cm}^3 \]

And so on.