Theorem of the Apothems in a Right Pyramid

In a right pyramid, the heights of the lateral faces (apothems) are congruent and pass through the points where the inscribed circle is tangent to the sides of the base.

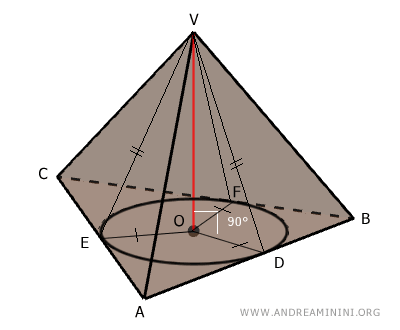
The altitudes of the lateral faces are the perpendicular segments dropped from the pyramid’s apex to the edges of the base.

This theorem states that these altitudes are all congruent and intersect the base at the points of tangency between the inscribed circle and the base’s sides.

Why does this matter?

The theorem guarantees that the lateral faces of a right pyramid exhibit symmetry, and it provides a straightforward way to compute their altitudes when the radius of the inscribed circle is known.

Note. In particular, if the base is a regular polygon, the lengths of the lateral altitudes can be determined using simple geometric formulas.

Proof

Consider a right pyramid.

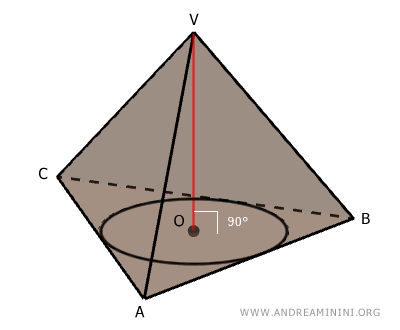
By definition, the segment $OV$ is perpendicular to the base plane $ABC$ of the pyramid.

Now, draw the segments connecting the center of the inscribed circle to the points of tangency $D, E,$ and $F$.

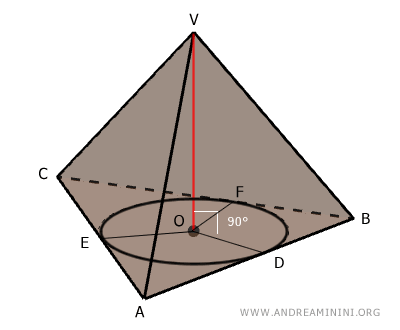
Since these are radii of the same circle, the segments $OD, OE,$ and $OF$ are congruent.

$$OD \cong OE \cong OF$$

Furthermore, because $D, E,$ and $F$ are points of tangency, the radii are perpendicular to the corresponding sides of the base:

$$OD \perp AB$$

$$OE \perp AC$$

$$OF \perp BC$$

Next, draw the segments connecting each tangency point $D, E,$ and $F$ to the pyramid’s apex $V$.

 

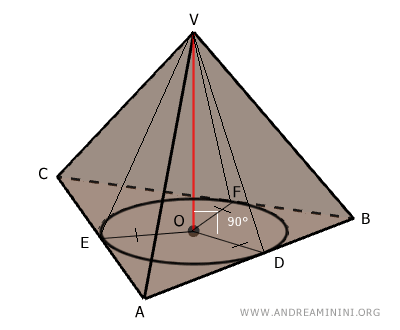
By the **Three Perpendiculars Theorem**, since $OV$ is perpendicular to the base $ABC$ and $OD$ is perpendicular to $AB$, it follows that $VD$ (lying in the lateral face) must also be perpendicular to $AB$.

$$VD \perp AB$$

Thus, $VD$ is the altitude of the lateral face $ABV$.

The same reasoning applies to the altitudes $VE$ and $VF$ of the other lateral faces:

$$VE \perp AC$$

$$VF \perp BC$$

Now, consider the triangles $OVD$ and $OVE$. These share a common side $OV$, have congruent sides $OD \cong OE$, and contain a right angle between them. By the Side-Angle-Side (SAS) Congruence Theorem, the two triangles are congruent:

$$OVD \cong OVE$$

Since congruent triangles have corresponding congruent parts, it follows that:

$$VD \cong VE$$

Thus, the altitudes of these two lateral faces are equal.

Repeating the same argument, we conclude that all lateral altitudes—including $VF$—are congruent.

Therefore, we have proven that in a right pyramid, the altitudes of all lateral faces are congruent.

Q.E.D. (Quod Erat Demonstrandum)