Frustum of a Pyramid

A frustum of a pyramid is a solid geometric figure created by cutting a pyramid with a plane parallel to its base. This cut results in a new face, smaller than the original base, and transforms the pyramid into a solid with two parallel bases.

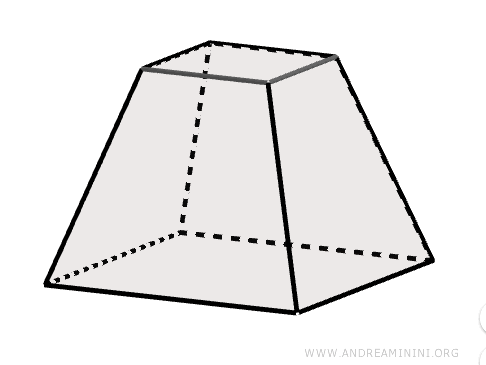
When a pyramid is intersected by a plane parallel to its base, it is divided into two distinct solids:

• A smaller pyramid at the top, with vertex \( V \) and base \( A'B'C'D' \). This new pyramid shares the same apex as the original pyramid \( ABCDV \), and the two figures are similar in shape.
• A truncated pyramid (or frustum), located at the bottom, bounded by two parallel polygonal bases and lateral faces that take the form of trapezoids.

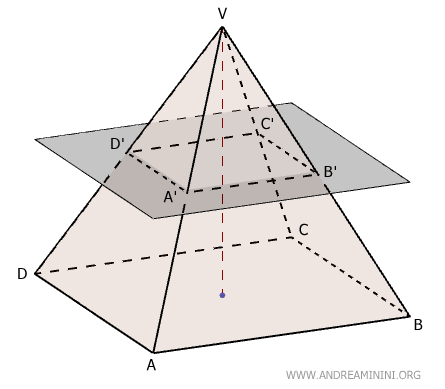
In a truncated pyramid, the bases are parallel and similar, though they differ in size.

The larger base (ABCD) is the original base of the pyramid, while the smaller base (A'B'C'D') is the cross-section created by the intersecting plane.

The lateral faces of the frustum are trapezoidal. In the special case of a regular pyramid, these lateral faces are isosceles trapezoids.

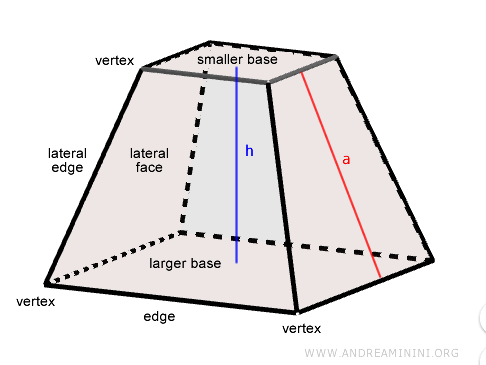
The number of lateral faces corresponds to the number of sides of the pyramid’s base.

This rule applies regardless of whether the pyramid’s base is a regular or irregular polygon.

The following principles, which apply to other polyhedral solids, are also relevant here:

• The height (h) is the perpendicular distance between the two bases.
• The vertices of the frustum are the vertices of both the larger and smaller bases.
• The lateral edges are the segments connecting the vertices of the two bases.
• The slant height (a) is used to calculate the lateral surface area.

A regular pyramid frustum is a frustum derived from a regular pyramid. It is characterized by congruent isosceles trapezoids as lateral faces, with the height of each trapezoid equal to the slant height of the frustum. A frustum is called a right frustum if it is derived from a right pyramid - one whose apex is exactly aligned with the center of the base and whose axis is perpendicular to the base plane.

Formulas

The formulas for calculating the surface area and volume of a pyramid frustum are as follows:

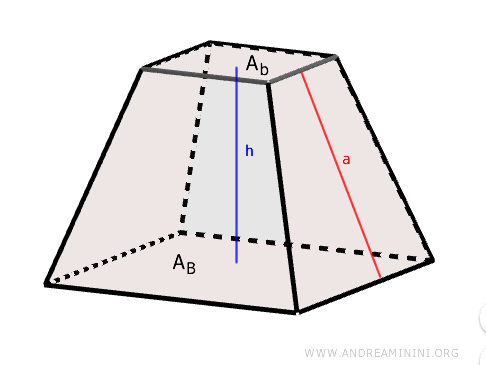
• Lateral Area (A_l)
  This is calculated by adding up the areas of all the lateral faces (trapezoids). Alternatively, it can be computed by multiplying the sum of the semi-perimeters of the bases by the slant height. $$ A_l = (p_B + p_b) \cdot a $$ where p_B and p_b are the semi-perimeters of the larger and smaller bases, respectively, and "a" is the slant height.

  Proof. Let's consider a right regular pyramid with a square base.
  
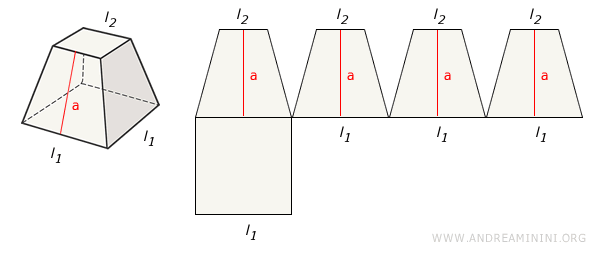
  The lateral surface area is the sum of the areas of the lateral faces. In this simplified case, all faces are congruent trapezoids, each with area given by $ \frac{(l_1+l_2) \cdot a}{2} $. This reasoning, however, holds more generally, even if the faces have different dimensions. $$ A_l = 4 \cdot \frac{(l_1+l_2) \cdot a}{2} $$ $$ A_l = \frac{(4l_1+4l_2) \cdot a}{2} $$ Here, $ P_B = 4l_1 $ represents the perimeter of the lower base of the truncated pyramid, and $ P_b = 4l_2 $ is the perimeter of the upper base. $$ A_l = \frac{(P_B + P_b) \cdot a}{2} $$ Since $ p_B = \frac{P_B}{2} $ is the semiperimeter of the lower base and $ p_b = \frac{P_b}{2} $ is the semiperimeter of the upper base, we can rewrite the formula as: $$ A_l = (p_B + p_b) \cdot a $$ Therefore, the lateral surface area is equal to the product of the sum of the semiperimeters of the two bases and the slant height (the apothem) of the truncated pyramid. As required.

• Total Area (A_t)
  This is the sum of the lateral area and the areas of the two bases. $$ A_t = A_B + A_b + A_l $$
• Volume (V)
  The volume is determined using the formula: $$ V = \frac{1}{3}h(A_B + A_b + \sqrt{A_B \cdot A_b}) $$ where \( h \) is the height of the frustum, \( A_B \) is the area of the larger base, and \( A_b \) is the area of the smaller base.

Additional Notes

Some remarks and observations on the frustum of a pyramid.

• The cross-section and the base are similar
  In a pyramid frustum, the base and any cross-section parallel to it are similar polygons.

  Proof. The base and the cross-section lie in two parallel planes, \( \pi \) and \( \pi' \), that intersect the lateral faces of the original pyramid. As a result, the corresponding sides of the base and the cross-section are parallel: $ AB \parallel A'B' $. The triangles \( VAB \) and \( VA'B' \) share the vertex \( V \).
  
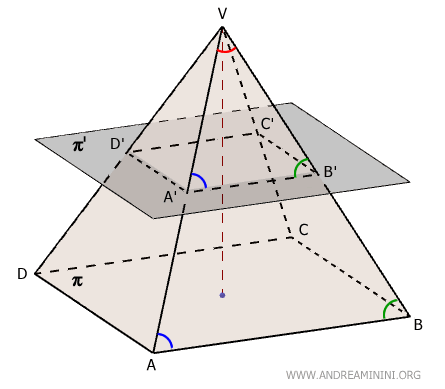
  Angles $ V \hat{A} B $ and $ V \hat{A'} B' $ are congruent by the parallel lines theorem, since \( AB \) and \( A'B' \) are parallel and are intersected by the same transversal line, namely \( VA \). By the same reasoning, angles \( V \hat{B} A \) and \( V \hat{B'} A' \) are congruent as well. Hence, triangles \( VAB \) and \( VA'B' \) are similar by the Angle-Angle-Angle (AAA) similarity criterion, as all corresponding angles are congruent in order. $$ VAB \approx VA'B' $$ This leads directly to the proportionality of corresponding sides: $$ AB : A'B' = VB : VB' $$ The same relationship holds for the other lateral faces: \( VBC \approx VB'C' \), \( VCD \approx VC'D' \), and \( VAD \approx VA'D' \), yielding: $$ BC : B'C' = VB : VB' $$ By transitivity: $$ AB : A'B' = VB : VB' = BC : B'C' $$ So we conclude: $$ AB : A'B' = BC : B'C' $$ This reasoning can be extended to all remaining lateral faces. Thus, not only are the corresponding sides of the base and the cross-section proportional, but their corresponding angles are also congruent, since they lie in planes that cut through the same dihedral angles of the pyramid.
  
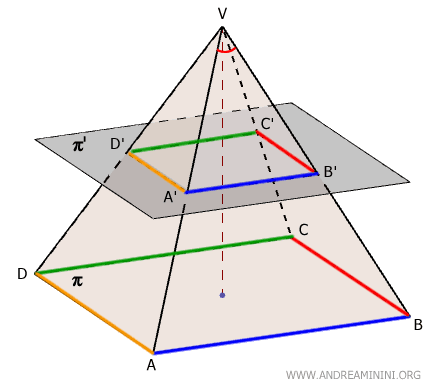
  Therefore, the base and the cross-section are similar polygons: $$ ABCD \approx A'B'C'D' $$

• Sides and perimeters scale proportionally with the distance from the vertex
  When a pyramid is intersected by a plane parallel to its base, the sides and perimeter of the resulting cross-sectional polygon are proportional to the distance between that plane and the vertex V.

  Proof. Triangles VAH and VA'H' are similar by the first similarity criterion, as they share the vertex angle at V and both contain a right angle (90°).
  
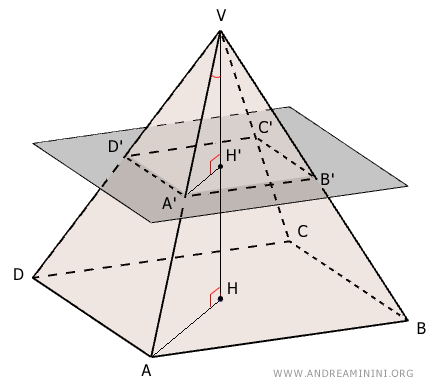
  Since $ VAH \approx VA'H' $, their corresponding sides are in proportion. In particular: $$ \frac{VH}{VH'} = \frac{VA}{VA'} $$ Similarly, triangles ABV and A'B'V are also similar by the same criterion. They share the angle at vertex V, and the base angles are congruent, $ V \hat{A} B \cong V \hat{A'} B' $, as guaranteed by the parallel lines theorem.
  
  Because $ ABV \approx A'B'V $, their corresponding sides also follow the same ratio: $$ \frac{AB}{A'B'} = \frac{VA}{VA'} $$ By transitivity, since $ \frac{VH}{VH'} = \frac{VA}{VA'} $, we can conclude: $$ \frac{AB}{A'B'} = \frac{VH}{VH'} $$ The same reasoning applies to all other corresponding sides of the base and the cross-section: $$ \frac{BC}{B'C'} = \frac{VH}{VH'} $$ $$ \frac{CD}{C'D'} = \frac{VH}{VH'} $$ $$ \frac{AD}{A'D'} = \frac{VH}{VH'} $$ Consequently, the perimeters of the two polygons are also in the same ratio: $$ \frac{AB + BC + CD + AD}{A'B' + B'C' + C'D' + A'D'} = \frac{VH}{VH'} $$ Let’s denote the perimeters as $2p$ and $2p'$: $$ \frac{2p}{2p'} = \frac{VH}{VH'} $$ From this, we see that the ratio of the perimeters matches the ratio of any pair of corresponding sides: $$ \frac{2p}{2p'} = \frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{CD}{C'D'} = \frac{AD}{A'D'} $$

• The ratio of the base area to the cross-sectional area equals the square of the similarity ratio
  In a truncated pyramid, the ratio between the area of the base S and that of the cross-section S' is equal to the square of the similarity ratio. \[ \frac{S}{S'} = \left( \frac{AB}{A'B'} \right)^2 = k^2 \]

  Proof. The base and the cross-section of a truncated pyramid are similar polygons. The ratio of the areas of two similar polygons, $ \frac{S}{S'} $, is equal to the square of the similarity ratio, $ k^2 $ (see proof). Therefore, in a truncated pyramid, the ratio between the base area and the cross-sectional area is given by the square of the similarity ratio $ k $.
  
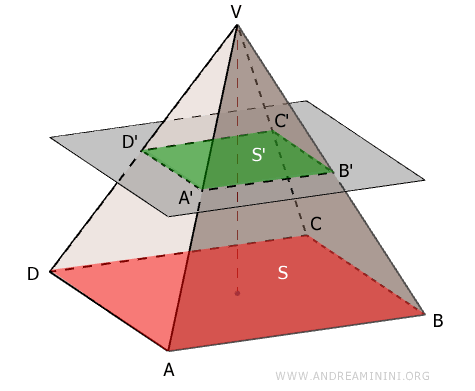
  For instance, consider a pyramid with a square base. The area of the base $ ABCD $ is the square of one of its sides: $ S = (AB)^2 $. Similarly, the area of the cross-section $ A'B'C'D' $ is $ S' = (A'B')^2 $. So the ratio of the two areas is: $$ \frac{S}{S'} = \frac{(AB)^2}{(A'B')^2} = \left( \frac{AB}{A'B'} \right)^2 = k^2 $$ where $ k = \frac{AB}{A'B'} $ is the similarity ratio between the two polygons. This property applies to all pairs of similar polygons, not just squares. In any two similar polygons, corresponding sides are in the same ratio $ k $, and all other linear measurements - such as heights, diagonals, and so on - scale proportionally by the same factor.

And that’s how it’s done.