Frustum of a Cone
A frustum of a cone is a solid shape formed by slicing the top off a cone with a plane parallel to its base.
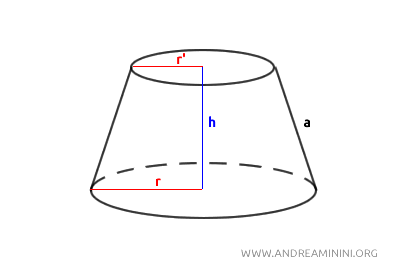
This process creates a geometric solid with two circular bases of different sizes: a larger base (the original base of the cone) and a smaller one (the cut surface).
The sides of the frustum are slanted, and if you extend the lines of the sides, they would meet at a point above the larger base.
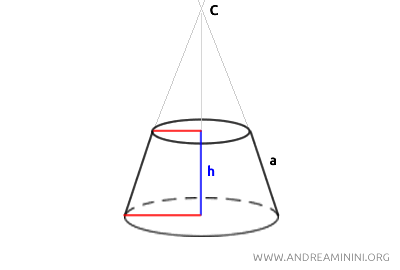
In other words, the imaginary lines you get by extending the slant height (a) of the cone converge at the point C, which is the projection of the cone’s original apex.
Properties of the Frustum of a Cone
A frustum of a cone is created by rotating a trapezoid 360° around the side perpendicular to its parallel sides, which corresponds to the height (h) of the solid.
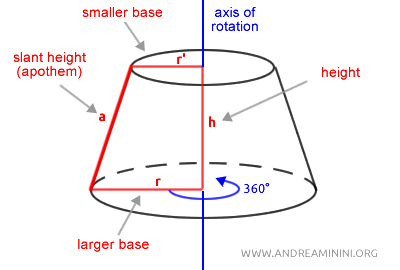
The line along which the trapezoid is rotated is called the axis of rotation.
The slanted side of the trapezoid becomes the slant height (a) of the frustum, which is the height of its lateral surface.
Note: This shape is quite common in various contexts, from mathematics to everyday objects like paper cups and lampshades. It also appears in architectural structures such as domes, towers, and chimneys, where the frustum shape is valued for its stability and aesthetic appeal. In addition, frustums are used in speaker design to improve sound directionality and transmission efficiency.
Formulas
The key dimensions of a frustum of a cone are its height (the vertical distance between the two bases), the radius of the larger base, and the radius of the smaller base.
- Base Area
The area of each base needs to be calculated separately because they have different radii (r ≠ r').
- Larger Base $$ A_B = \pi r^2 $$
- Smaller Base $$ A'_B = \pi r'^2 $$
Note. The sum of the base areas of a truncated cone is $$ A_B + A'_B = \pi r^2 +\ \pi r'^2 = \pi ( r^2 + r'^2 ) $$
- Lateral Surface Area
The lateral surface area AL is found using the slant height (a) of the frustum. $$ A_L = \pi a (r + r') $$Note. The lateral surface area of a truncated cone is equal to the product of the slant height and the sum of the semicircumferences of the two bases. $$ A_L = a \cdot ( \frac{1}{2} \cdot 2 \pi r + \frac{1}{2} \cdot 2 \pi r') $$ $$ A_L = a \cdot (\ \pi r +\ \pi r') $$ $$ A_L = a \cdot \pi \cdot (r +\ r') $$
- Total Surface Area
The total surface area is the sum of the lateral surface area and the areas of both bases: $$ A_T = A_L + A_B + A'_B $$ - Volume
The volume of the frustum is calculated with the formula: $$ V = \frac{1}{3} \pi h (r^2 + r'^2 + r \cdot r') $$ where h is the height of the frustum, r is the radius of the larger base, and r' is the radius of the smaller base.Proof. Consider a large cone with radius $ R $ and height $ H $. We remove from it a smaller cone with radius $ r' $ and height $ h'$.
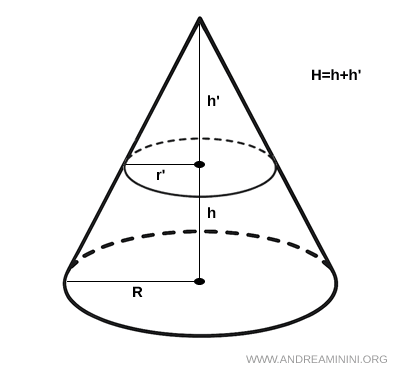
Since the two cones are similar, the following proportion holds: $$ r':R = h':H $$ where $ H = h + h' $, as the total height is the sum of the height of the smaller cone and that of the frustum. $$ r':R = h':(h + h') $$ Expressing this as a fraction gives: $$ \frac{r'}{R} = \frac{h'}{H} = \frac{h'}{h + h'} $$ Solving for the height $ h' $ of the smaller cone: $$ \frac{r'}{R} = \frac{h'}{h + h'} $$ $$ r'(h + h') = R h' $$ $$ r'h + r'h' = R h' $$ $$ r'h = h'(R - r') $$ $$ h' = \frac{r'}{R - r'} \cdot h $$ Now let’s compute the volumes of the two cones:- $V_1 = \frac{1}{3} \pi R^2 (h + h')$ (volume of the large cone)
- $V_2 = \frac{1}{3} \pi r'^2 h'$ (volume of the small cone)
Relationship Between the Areas of Circles in a Cone and Their Distances from the Vertex
In a truncated cone, the area of the base circle and that of a circular cross-section taken parallel to the base are proportional to the squares of their respective distances from the vertex. \[\frac{A_1}{A_2} = \left( \frac{h_1}{h_2} \right)^2 \]
Where:
- \( A_1 \) is the area of the base circle (the larger one);
- \( A_2 \) is the area of the circle from the parallel cross-section (the smaller one);
- \( h_1 \) is the distance from the vertex to the base plane;
- \( h_2 \) is the distance from the vertex to the plane of the cross-section.
When a cone is sliced by a plane parallel to its base, the resulting cross-section is a smaller circle that is geometrically similar to the base circle.
In similar figures, corresponding linear dimensions scale proportionally, while areas scale with the square of the ratio and volumes with the cube.
As a result, the areas of the base circle and the cross-sectional circle follow a precise mathematical relationship based on their distances from the cone’s vertex.
Practical Example
Consider a truncated cone whose original height is \( h_1 = 12 \, \text{cm} \)
and where the cross-section is taken at \( h_2 = 4 \, \text{cm} \) from the vertex.
The ratio of the two areas will be:
\[ \frac{A_1}{A_2} = \left( \frac{12}{4} \right)^2 = 3^2 = 9 \]
From this, we conclude that:
\[ A_1 = 9 \cdot A_2 \]
In plain terms: the base circle has an area nine times greater than that of the smaller, upper circle.
Proof
Let’s consider a cone and a cross-section taken parallel to its base.
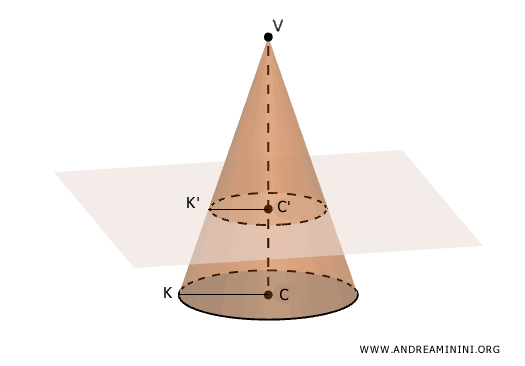
The triangles VCK and VC'K' are similar according to the first criterion of triangle similarity, since their corresponding angles are congruent.
It follows that their corresponding sides are in proportion:
$$ VC : VC' = CK : C'K' $$
which can be expressed as:
$$ \frac{VC}{VC'} = \frac{CK}{C'K'} $$
Squaring both sides yields:
$$ \left( \frac{VC}{VC'} \right)^2 = \left( \frac{CK}{C'K'} \right)^2 $$
$$ \frac{VC^2}{VC'^2} = \frac{CK^2}{C'K'^2} $$
Since the area of a circle is given by \( A = \pi r^2 \), the ratio of the two areas is equal to the square of the ratio of their radii:
$$ \frac{ \pi \cdot (CK)^2}{ \pi \cdot (C'K')^2} = \frac{ CK^2 }{ C'K'^2 } $$
Where \( A = \pi \cdot (CK)^2 \) is the area of the base circle, and \( A_s = \pi \cdot (C'K')^2 \) is the area of the cross-sectional circle.
Therefore,
$$ \frac{ A}{ A_s} = \frac{ CK^2 }{ C'K'^2 } $$
By transitivity, the ratio of the areas equals the ratio of the squares of their distances from the cone’s vertex:
$$ \frac{VC^2}{VC'^2} = \frac{CK^2}{C'K'^2} = \frac{ A}{ A_s} $$
$$ \frac{VC^2}{VC'^2} = \frac{ A}{ A_s} $$
Which completes the proof.
And so on.
