Parallel Sections of a Dihedral Angle

In a dihedral angle, parallel sections are congruent.

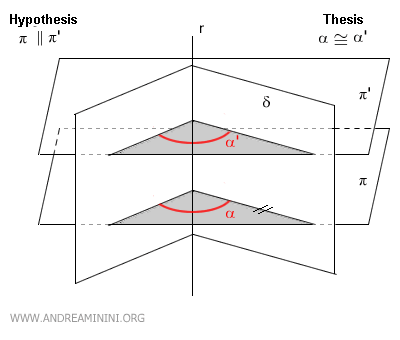
For example, let the plane π intersect the dihedral angle, forming an angle α.

Another plane π', which is parallel to π (i.e., π||π'), also intersects the dihedral angle, forming a congruent angle α≅α'.

Since the dihedral angle remains the same, the two parallel sections are congruent.

Proof

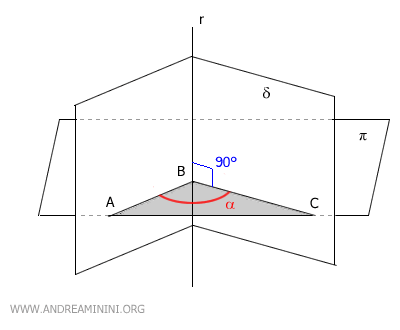
Consider the dihedral angle δ and a plane π that intersects it along the edge r (a normal section).

For simplicity, let’s use a plane that is perpendicular to the edge (90°), although any other inclination would work just as well.

The plane π intersects the dihedral angle δ at points A, B, and C.

Now, let’s consider another plane π', which is parallel to π.

This plane π' intersects the dihedral angle at points A', B', and C'.

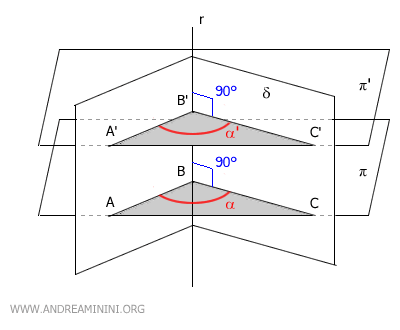
Since the two planes are parallel, the quadrilaterals AA'B'B and BB'C'C are parallelograms.

Knowing that in a parallelogram, opposite sides are congruent, we can deduce that AA'≅BB', AB≅A'B', BB'≅CC', and BC≅B'C'.

Furthermore, by the transitive property, since AA'≅BB' and BB'≅CC', we can conclude that AA'≅CC'.

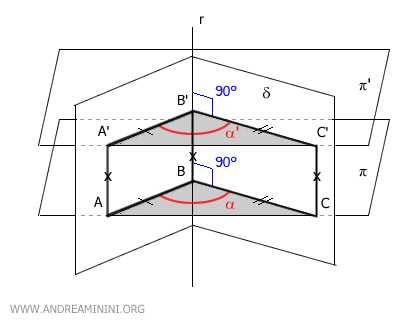
Having established that the sides AA'≅CC' are congruent, it follows that AA'C'C forms a parallelogram as well.

Thus, the slanting sides of the parallelogram, AC≅A'C', are congruent.

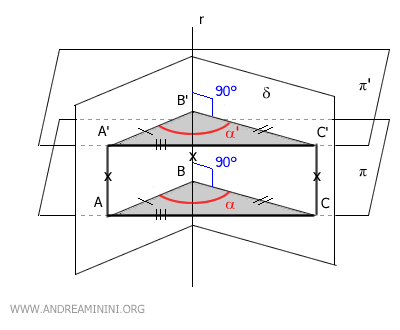
At this point, we can observe that the triangles ABC and A'B'C' are congruent by the SSS congruence criterion (side-side-side), as all their corresponding sides are congruent: AC≅A'C', AB≅A'B', and BC≅B'C'.

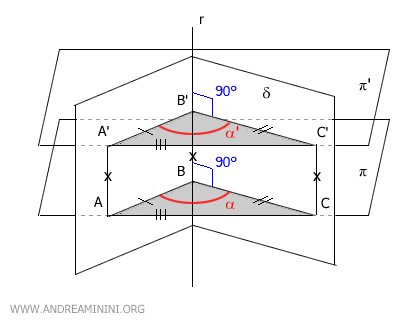
Since the two triangles are congruent, all their corresponding angles are also congruent.

In particular, the angles α≅α' are congruent, which proves that the parallel sections of the dihedral angle δ are congruent.

$$ \alpha \cong \alpha ' $$

The theorem is thus proven.

And so forth.