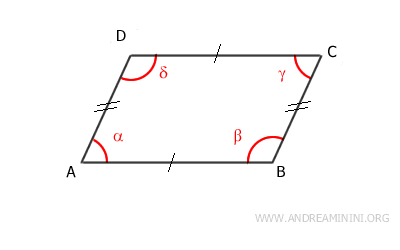
Parallelogram
A parallelogram is a four-sided flat geometric figure (a quadrilateral) where opposite sides are parallel and equal in length (congruent).
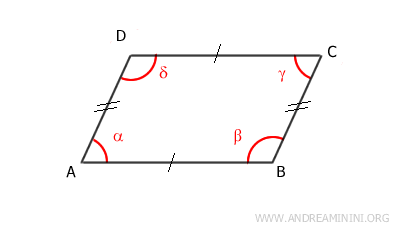
Here are some key properties of parallelograms:
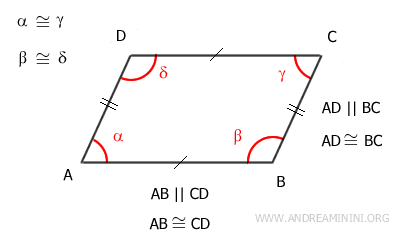
- Opposite sides are parallel and congruent.
- Opposite angles are congruent and have the same measure.
- Adjacent angles on the same side are supplementary, adding up to 180°.
- The diagonals intersect at their midpoint.
- Each diagonal divides the parallelogram into two congruent triangles.
Common examples of parallelograms include rectangles and rhombuses, which are special cases with additional properties.
A parallelogram is a convex geometric figure because it can be viewed as the intersection of two non-parallel strips.
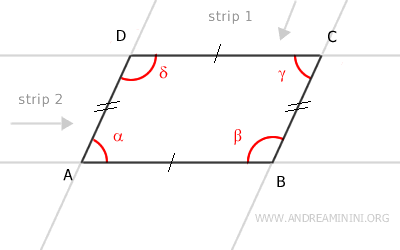
A "strip" refers to the area of the plane between two parallel lines.
Key Formulas for Parallelograms
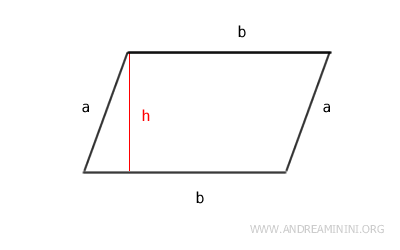
- The perimeter of a parallelogram is twice the sum of the base (b) and the slant height (a). $$ P = 2 \cdot (a+b) $$
- The area of a parallelogram is calculated by multiplying the base (b) by the height (h): $$ A = b \cdot h $$
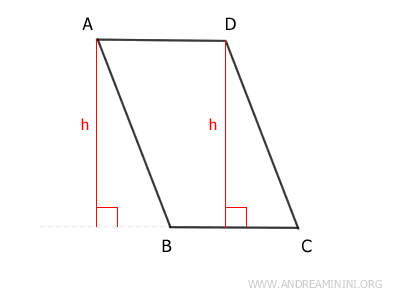
The Base and Height of a Parallelogram
In a parallelogram, any side can be considered the base (b), with one of its adjacent sides serving as the height (h).
The height (h) is the perpendicular distance between the side opposite the base and the line that contains the base.
For example, the segment h is the height of parallelogram ABCD when side AB is chosen as the base.
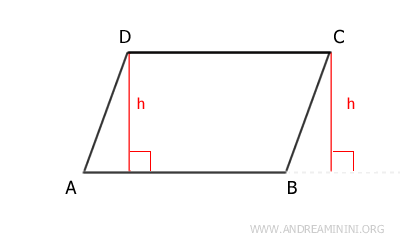
Conversely, if side BC is chosen as the base, the heights (h) of the parallelogram are shown below:
Types of Parallelograms
Parallelograms include various common geometric shapes, such as rectangles, rhombuses, and squares.
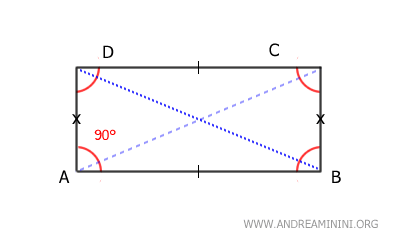
- Rectangles
Rectangles are a type of parallelogram characterized by four right angles (90°).
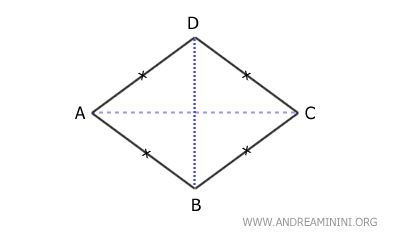
- Rhombuses
Rhombuses are parallelograms where all sides are of equal length, and their diagonals are perpendicular to each other.
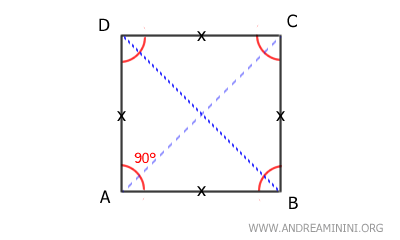
- Squares
Squares are special parallelograms that combine the properties of both rectangles and rhombuses. They have four right angles, equal sides, and diagonals that intersect at right angles.
Thus, rectangles, rhombuses, and squares are specific types of parallelograms.
The main differences among these shapes are summarized in the table below:
| Property | Parallelogram | Rectangle | Rhombus | Square |
|---|---|---|---|---|
| Opposite sides congruent | YES | YES | YES | YES |
| Opposite angles congruent | YES | YES | YES | YES |
| Adjacent angles supplementary | YES | YES | YES | YES |
| Diagonals meet at their midpoint | YES | YES | YES | YES |
| Diagonals divide into congruent triangles | YES | YES | YES | YES |
| Diagonals are congruent | -- | YES | -- | YES |
| Diagonals are perpendicular | -- | -- | YES | YES |
| Diagonals bisect angles | -- | -- | YES | YES |
| All sides congruent | -- | -- | YES | YES |
| Sum of interior angles is 360° | YES | YES | YES | YES |
Parallelogram Theorem
A convex quadrilateral is a parallelogram if it meets one of the following criteria:
- Opposite sides are congruent.
- Opposite angles are congruent.
- The diagonals intersect at their midpoint.
- Two opposite sides are both congruent and parallel.
If any one of these conditions is met, the others are automatically satisfied.
Therefore, to determine whether a quadrilateral is a parallelogram, it is enough to verify if at least one of these conditions is true.
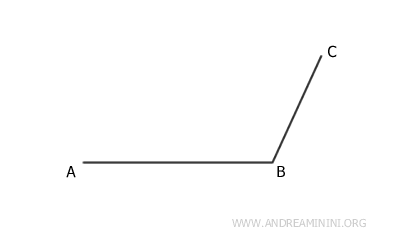
How to Construct a Parallelogram
First, draw two consecutive sides of the parallelogram.
Start by drawing the longer side AB followed by the shorter side BC (or vice versa).
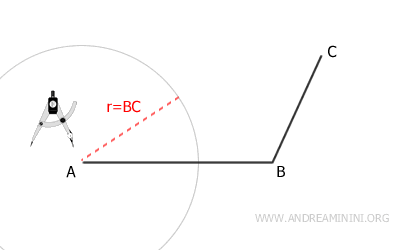
Place the compass at vertex A, and with a radius equal to BC, draw the first arc.
Then, place the compass at vertex C, and with a radius equal to AB, draw the second arc.
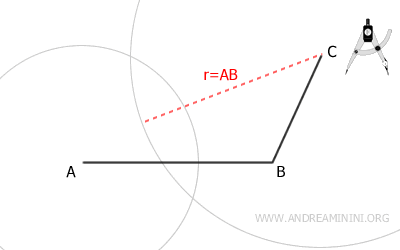
The two arcs can intersect at two distinct points: D and E.
However, only one of these points (D) will result in a convex polygon, so the other point (E) can be ignored.
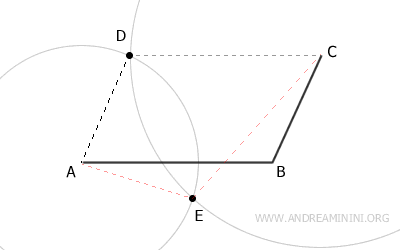
In this case, point D is the fourth vertex of the parallelogram.
Now, draw segment CD.
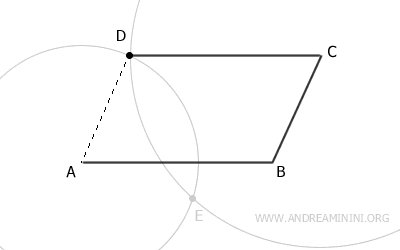
Finally, draw segment AD, the fourth and final side of the quadrilateral.
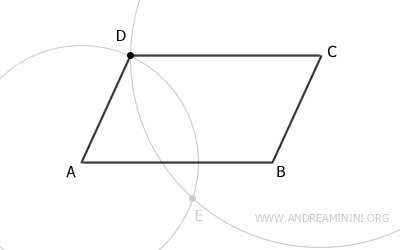
The result is a parallelogram, a quadrilateral with opposite sides that are both parallel and congruent.
Observations
Some important notes and properties regarding parallelograms:
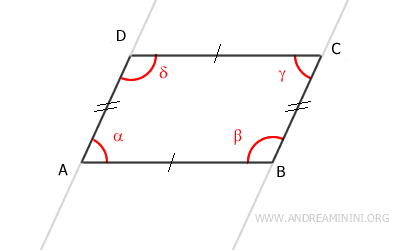
- Each side and diagonal of the parallelogram can be considered a transversal cutting through two parallel lines.
This allows the use of parallel line theorems to determine the angles of the parallelogram or in geometric proofs.
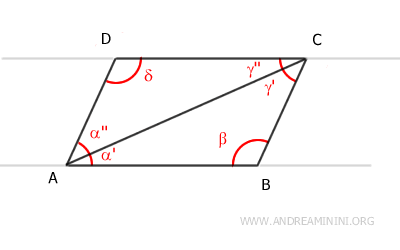
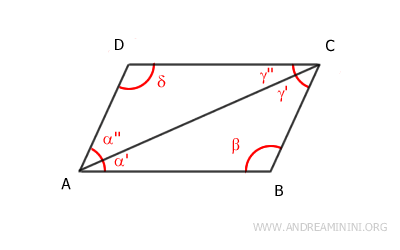
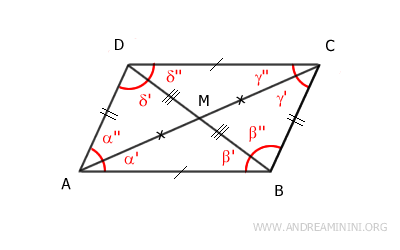
- Each diagonal divides the parallelogram into two congruent triangles
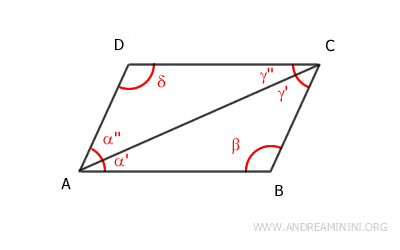
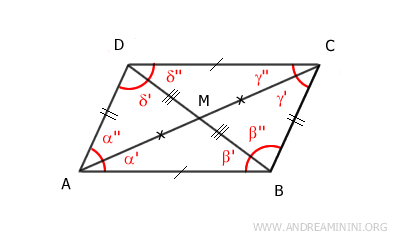
Proof: Consider the longer diagonal from vertex A to vertex C. This diagonal divides the parallelogram into two triangles, ACD and ABC. The diagonal AC is a shared side for both triangles. According to the parallel lines theorem, angles α' and γ'' are congruent α'≅γ'' because they are alternate interior angles formed by segments AB and CD intersected by transversal AC. Similarly, angles α'' and γ' are congruent α''≅γ' for the same reason - they are also alternate interior angles. Therefore, by the second congruence criterion (ASA), the two triangles ACD and ABC are congruent ACD≅ABC.
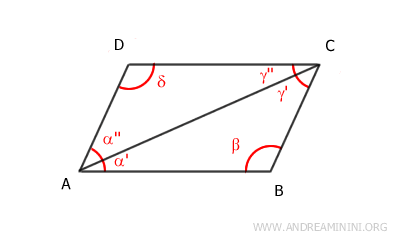
Now, consider the shorter diagonal from vertex B to vertex D. This diagonal divides the parallelogram into two triangles, ABD and BCD. The diagonal BD is a shared side for both triangles. According to the parallel lines theorem, angles β' and δ'' are congruent β'≅δ'' because they are alternate interior angles formed by segments AB and CD intersected by transversal BD. Similarly, angles β'' and δ' are congruent β''≅δ' for the same reason - they are also alternate interior angles. Therefore, by the second congruence criterion (ASA), the two triangles ABD and BCD are congruent ABD≅BCD.
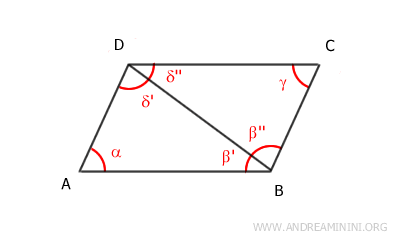
- Opposite sides of a parallelogram are congruent
Proof: A diagonal divides the parallelogram into two congruent triangles: ACD≅ABC. Since these triangles are congruent, the corresponding sides of the two triangles are congruent in the same order: CD≅AB, AD≅BC, with AC being the shared side. This proves the congruence of the opposite sides of the parallelogram.
- Opposite angles of a parallelogram are congruent
Proof: The longer diagonal AC divides the parallelogram into two congruent triangles: ACD≅ABC. As a result, the corresponding angles of these triangles are congruent: β≅δ, γ'≅α'', α'≅γ''. Specifically, it is important to note that angles β≅δ are congruent because they are opposite angles of the parallelogram.
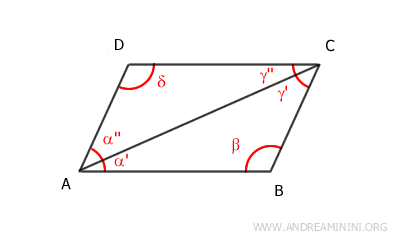
Similarly, the shorter diagonal BD divides the parallelogram into two congruent triangles: ADB≅BCD. Again, in this case, the corresponding angles of the two triangles are congruent: α≅γ, β'≅δ'', δ'≅β''. Specifically, it is important to note that angles α≅γ are congruent because they are opposite angles of the parallelogram.
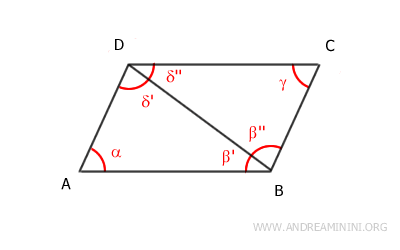
- Adjacent angles in a parallelogram are supplementary (180°)
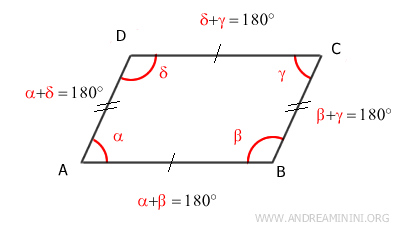
Proof: Angles α and β are adjacent to side AB. According to the parallel lines theorem, angles α and β are supplementary (α+β=180°) because they are corresponding angles of parallel lines AD||BC intersected by transversal AB. The same reasoning applies to all other adjacent angles in the parallelogram.
This demonstrates that all adjacent angles in a parallelogram are supplementary angles $$ \alpha + \beta = 180° $$ $$ \alpha + \delta = 180° $$ $$ \beta + \gamma = 180° $$ $$ \gamma + \delta = 180° $$ - The diagonals intersect at their midpoint
Proof: Draw the two diagonals AC and BD of the parallelogram. The opposite sides of the parallelogram are congruent AB≅CD and AD≅BC. According to the parallel lines theorem, angles α'≅γ'' are congruent because they are alternate interior angles formed by the parallel lines AB||CD intersected by line AC. Similarly, angles β'≅δ'' are congruent because they are alternate interior angles formed by the parallel lines AB||CD intersected by line BD.
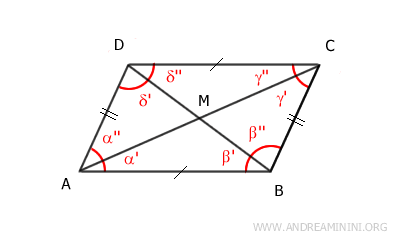
Therefore, by the second triangle congruence criterion, triangles ABM and CDM are congruent because they have one congruent side AB≅CD and two congruent angles α'≅γ'' and β'≅δ''. Thus, the corresponding sides of these triangles are congruent. Specifically, it is important to note that segments AM≅MC and BM≅DM are congruent. This means that point M is the midpoint of diagonals AC and BD, dividing both diagonals into two equal segments.
And so on.
