Parallelogram Theorem

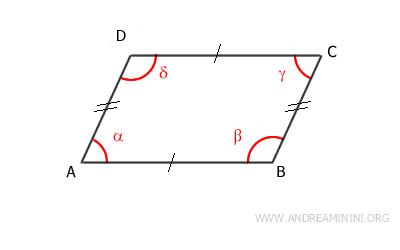
Meeting any one of these conditions is sufficient to determine if a quadrilateral is a parallelogram.

If one condition is met, the others are automatically satisfied as well.

Note: It’s crucial to emphasize that "convex" is a key term here because a parallelogram is, by definition, a convex quadrilateral with opposite sides that are both congruent and parallel.

Proof

The proof is divided into four main points.

1] A quadrilateral is a parallelogram if its opposite sides are congruent

In this scenario, the initial assumption is that the opposite sides are congruent: AB≅CD and AD≅BC.

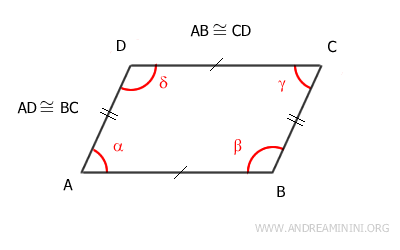
To prove that the quadrilateral is a parallelogram (the conclusion), I need to demonstrate that its opposite sides are not only congruent but also parallel.

Let's draw a diagonal connecting two vertices of the quadrilateral, for example, the diagonal AC.

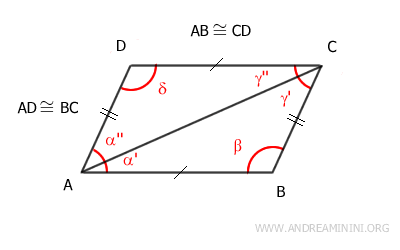
This diagonal divides the quadrilateral into two triangles: ABC and ACD.

The triangles ABC and ACD are congruent according to the third criterion of triangle congruence because they share:

• A common side (AC)
• Two pairs of congruent sides as per the initial assumption: AB≅CD and AD≅BC

Since the two triangles are congruent:

$$ ABC \cong ACD $$

We can conclude that they also have congruent angles in the corresponding positions:

$$ \alpha ' = \gamma '' $$

$$ \alpha '' = \gamma ' $$

$$ \delta = \beta $$

The angles α'≅γ'' are congruent and are also alternate interior angles formed by lines AB and CD being intersected by the transversal AC.

According to the converse of the parallel line theorem, alternate interior angles are congruent only if the transversal intersects two parallel lines.

Thus, lines AB and CD are parallel: AB||CD.

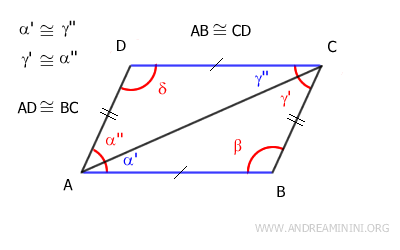
Similarly, the angles γ'≅α'' are congruent and are also alternate interior angles formed by lines AD and BC being intersected by the transversal AC.

Again, by the converse of the parallel line theorem, lines AD and BC are parallel: AD||BC.

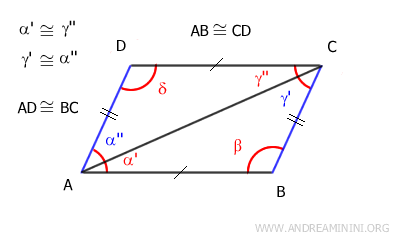
Having demonstrated that segments AB||CD and AD||BC are parallel, and knowing from the initial assumption that segments AB≅CD and AD≅BC are congruent, we can conclude that the quadrilateral is a parallelogram.

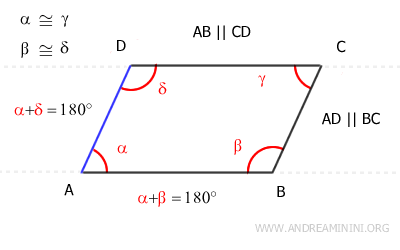
2] A quadrilateral is a parallelogram if its opposite angles are congruent 

Here, the initial assumption is that the opposite angles are congruent: α≅γ and β≅δ.

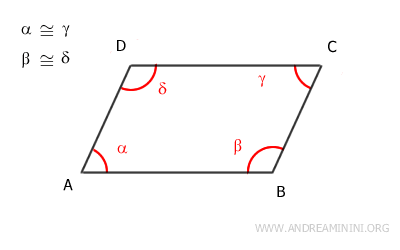
To establish that this is a parallelogram, I must show that the opposite sides are both parallel and congruent.

This is a convex polygon with four sides (n=4). Thus, the sum of its interior angles is (n-2)·180°=360°.

$$ \alpha + \beta + \gamma + \delta = 360° $$

Given the initial assumption that the angles α≅γ and β≅δ are congruent,

We know that the sum of congruent angles is also congruent, so we can write:

$$ \alpha + \beta \cong \gamma + \delta $$

$$ \alpha + \delta \cong \gamma + \beta $$

Knowing that α+β+γ+δ=360°, we deduce that the sums α+β=180° and α+δ=180° are true.

$$ \alpha + \beta = 180° $$

$$ \alpha + \delta = 180° $$

Thus, angles α and β, as well as angles α and δ, are supplementary because α+β=180° and α+δ=180°.

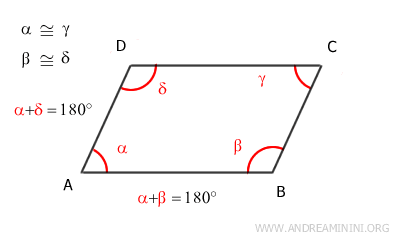
The angles α and β are supplementary angles (α+δ=180°) and are also consecutive interior angles formed by the intersection of lines AD and BC with the transversal AB.

Therefore, according to the converse of the parallel line theorem, the sides AD and BC of the quadrilateral are parallel, so AD||BC.

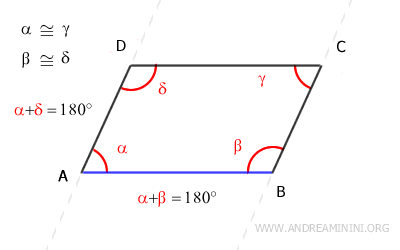
Likewise, angles α and δ are supplementary angles (α+δ=180°) and are also consecutive interior angles formed by the intersection of lines AB and CD with the transversal AD.

So, again by the converse of the parallel line theorem, sides AB and CD of the quadrilateral are parallel, so AB||CD.

After establishing that the opposite sides of the quadrilateral are parallel (AB||CD and AD||BC), the next step is to prove that these opposite sides are also congruent.

To do so, let’s draw the diagonal AC, which divides the quadrilateral into two triangles: ABC and ACD.

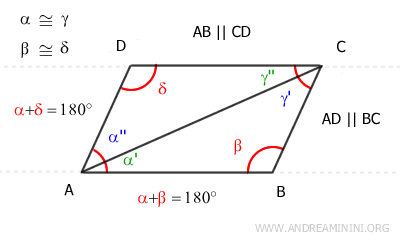
At this point, we apply the parallel line theorem:

• Since lines AD and BC are parallel, the alternate interior angles α''≅γ' formed by the intersection with the transversal AC are congruent.
• Similarly, since lines AB and CD are parallel, the alternate interior angles α'≅γ'' formed by the intersection with the transversal AC are congruent.

This allows us to state that triangles ABC and ACD are congruent by the second criterion of triangle congruence because:

• The two triangles share a common side (AC).
• The two triangles have two congruent angles α'≅γ'' and γ'≅α''.

Once we establish that triangles ABC≅ACD are congruent, it follows that their corresponding sides are congruent.

In particular, this means that sides AD≅BC and AB≅CD are congruent.

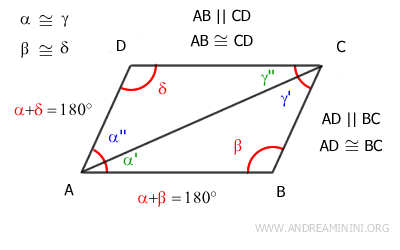
In conclusion, we have demonstrated that the opposite sides of the quadrilateral are both parallel and congruent.

Therefore, the quadrilateral is indeed a parallelogram.

3] A quadrilateral has two opposite sides that are both parallel and congruent

In this case, the initial assumption is that two opposite sides are both parallel and congruent.

For example, AB≅CD and AB || CD.

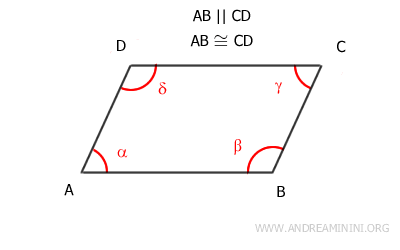
The goal is to demonstrate that the other two opposite sides, AD and BC, are also parallel and congruent.

We can start by drawing a diagonal AC, which divides the quadrilateral into two triangles: ABC and ACD.

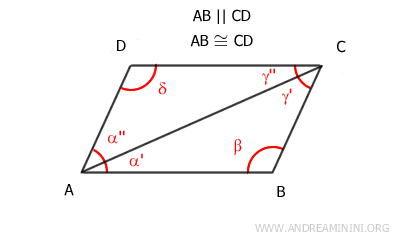
Since segments AB and CD are parallel by the initial assumption (AB || CD), according to the parallel line theorem, the alternate interior angles α'≅γ' are congruent.

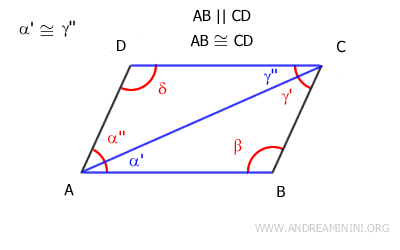
This allows us to conclude that the two triangles, ABC and ACD, are congruent based on the first criterion of triangle congruence because:

• They have a congruent side AB≅CD as per the initial assumption.
• They share the side AC (the diagonal).
• They have the angle α'≅γ' between the congruent sides.

Once we establish that triangles ABC≅ACD are congruent, it follows that all corresponding sides and angles are congruent.

In particular, this means that sides AD≅BC are congruent and that angles α''≅γ' are also congruent.

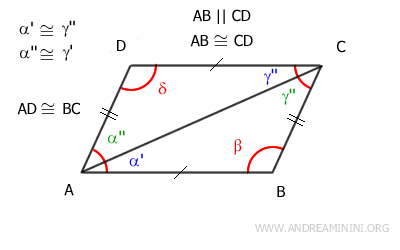
At this point, we have demonstrated that all opposite sides are congruent: AB≅CD and AD≅BC.

It remains to prove that sides AD and BC are also parallel.

To do so, note that angles α''≅γ' are congruent and are also alternate interior angles formed by the intersection of lines AD and BC with the transversal AC.

Thus, by the converse of the parallel line theorem, sides AD and BC are parallel: AD || BC.

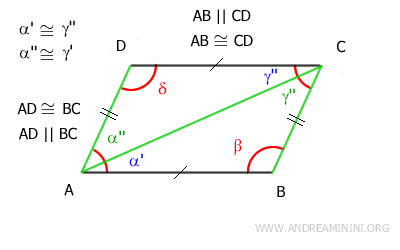
In conclusion, we have shown that the opposite sides of the quadrilateral are both parallel and congruent.

Therefore, the quadrilateral is a parallelogram.

4] A quadrilateral is a parallelogram if its diagonals bisect each other

The initial assumption is that the diagonals of the convex quadrilateral intersect at their midpoint.

Thus, segments AM≅CM and BM≅DM are congruent.

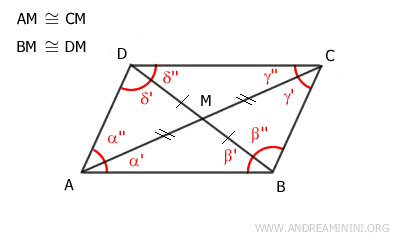
To prove that the quadrilateral is a parallelogram, we need to show that the opposite sides are parallel and congruent.

Angles θ' and θ'' are vertical angles, so they are congruent: θ'≅θ''.

This allows us to conclude that triangles AMD and BMD are congruent by the first criterion of triangle congruence, because they have two congruent sides and the included angle is congruent.

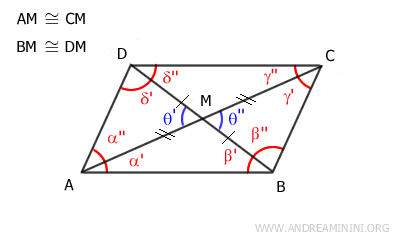
Once we establish that triangles AMD≅BMC are congruent, it follows that sides AD≅BC are congruent.

Furthermore, all the angles of the two triangles are congruent in corresponding order.

In particular, it’s important to note that angles δ'≅β' are congruent because they are also alternate interior angles formed by the intersection of lines AD and BC with the transversal BD.

Therefore, by the converse of the parallel line theorem, sides AD and BC are also parallel: AD || BC.

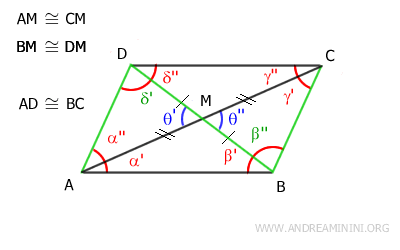
We can apply the same reasoning to triangles ABM and CDM.

Angles φ' and φ'' are vertical angles, so they are congruent: φ'≡φ''.

As a result, triangles ABM and CDM are congruent by the first criterion of triangle congruence because they have two congruent sides and the included angle is congruent.

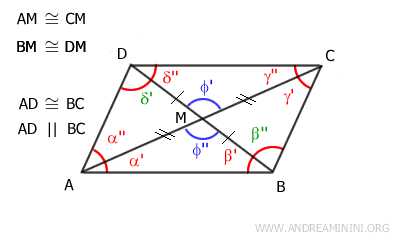
Once it is established that triangles ABM≅CDM are congruent, we conclude that sides AB≅CD are congruent.

Furthermore, the angles of the two triangles are congruent in corresponding order.

Specifically, it is useful to know that angles α'≅γ'' are congruent because they are also alternate interior angles formed by the intersection of lines AB and CD with the transversal AC.

Therefore, by the converse of the parallel line theorem, sides AB and CD are also parallel: AB || CD.

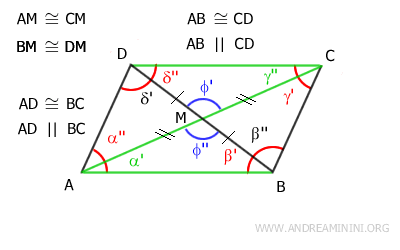
In conclusion, the opposite sides of the quadrilateral are both congruent and parallel.

Thus, we can confidently state that the quadrilateral is a parallelogram.

And so forth.