Rhombus

A rhombus is a type of parallelogram where all sides are of equal length.

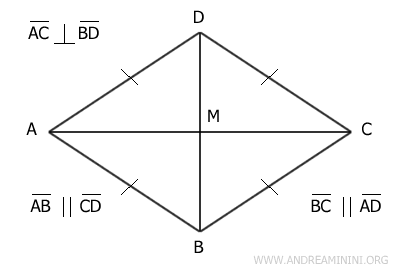
In simpler terms, a rhombus is a quadrilateral with four equal sides.

As a parallelogram, the rhombus shares all the fundamental properties of parallelograms:

• Opposite sides are parallel.
• Opposite angles and sides are congruent.
• Adjacent angles are supplementary.
• The diagonals bisect each other at their midpoints.

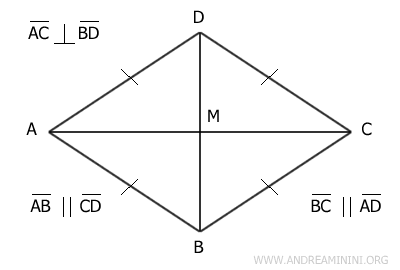
In addition, a rhombus has several distinct characteristics:

• All four sides are of equal length.
• The diagonals are perpendicular, forming a 90° angle.
• The diagonals bisect the interior angles.

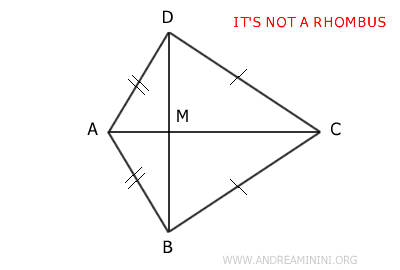
While these conditions are necessary, they alone do not guarantee that a quadrilateral is a rhombus.

For instance, a quadrilateral can have perpendicular diagonals without being a rhombus (e.g., a convex kite). To be classified as a rhombus, the shape must also be a parallelogram.

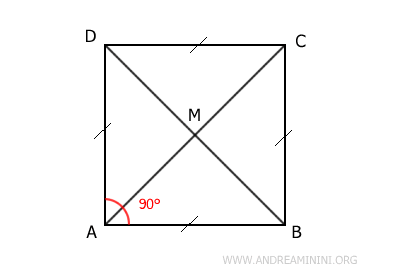
Additionally, a square possesses all the properties of a rhombus but differs by having four right angles of 90°. Thus, a square can be viewed as a specific type of rhombus. However, in common usage, a figure with these attributes is typically referred to as a 'square.'

Rhombus Formulas

Here are some key formulas for calculating various elements of a rhombus:

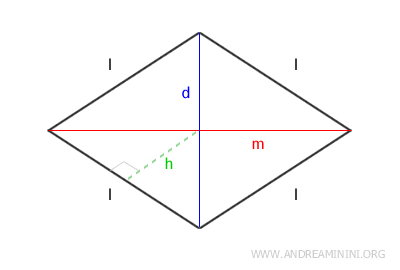
• Perimeter
  The perimeter of a rhombus is four times the length of one side. $$ P = 4 \cdot l $$
• Area
  The area of a rhombus can be calculated by multiplying the lengths of the diagonals (d and m) and then dividing by two. $$ A = \frac{d \cdot m}{2} $$ Alternatively, since a rhombus is a parallelogram, the area can also be found by multiplying a side length (l) by the height (h). $$ A = l \cdot h $$
• Side Length
  The side length can be determined using the Pythagorean theorem. $$ l = \sqrt{ ( \frac{d}{2})^2 + ( \frac{m}{2})^2 } $$
• Longer Diagonal
  The formula for the longer diagonal is derived from the side length formula. $$ d = 2 \cdot \sqrt{ l^2 - (\frac{m}{2})^2 } $$
• Shorter Diagonal
  The formula for the shorter diagonal can be similarly derived from the side length formula. $$ m = 2 \cdot \sqrt{ l^2 - (\frac{d}{2})^2 } $$

  Explanation. The algebraic steps to derive the formulas for the longer and shorter diagonals of a rhombus are straightforward. However, for completeness, I'll outline them below. For example, to calculate the longer diagonal, start with the side length formula: $$ l = \sqrt{ ( \frac{d}{2})^2 + ( \frac{m}{2})^2 } $$ Extract the (d/l)² term from the square root: $$ l = \frac{d}{2} + \sqrt{ ( \frac{m}{2})^2 } $$ Solve for the longer diagonal: $$ - \frac{d}{2} = -l + \sqrt{ ( \frac{m}{2})^2 } $$ Apply the property of invariance in equations and multiply both sides by -1: $$ - \frac{d}{2} \cdot (-1) = [ -l + \sqrt{ ( \frac{m}{2})^2 } ] \cdot (-1) $$ $$ \frac{d}{2} = l - \sqrt{ ( \frac{m}{2})^2 } $$ Move the side length term (l) inside the square root: $$ \frac{d}{2} = \sqrt{ l^2 - ( \frac{m}{2})^2 } $$ Finally, apply the property of invariance again and multiply both sides by two: $$ 2 \cdot \frac{d}{2} = 2 \cdot \sqrt{ l^2 - ( \frac{m}{2})^2 } $$ The final result is the formula for the longer diagonal: $$ d = 2 \cdot \sqrt{ l^2 - ( \frac{m}{2})^2 } $$ The same process can be repeated to derive the formula for the shorter diagonal: $$ m = 2 \cdot \sqrt{ l^2 - (\frac{d}{2})^2 } $$

How to Draw a Rhombus

Suppose you want to draw a rhombus with a primary diagonal of 6 units and a secondary diagonal of 4 units.

Start by drawing a line segment AB that is 6 units long, representing the primary diagonal of the rhombus.

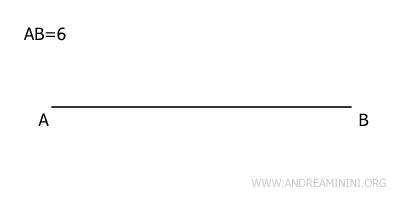
Next, draw a line perpendicular to segment AB.

With a compass set to a width slightly greater than half of AB, place the compass point at point A and draw an arc.

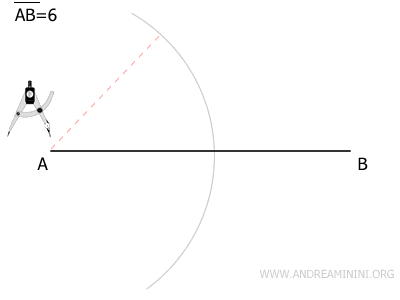
Without adjusting the compass, place the point at B and draw another arc that intersects the first at two distinct points.

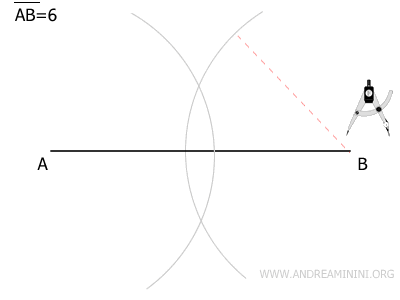
Draw a straight line through the points where the arcs intersect. This line is perpendicular to segment AB.

The point where the perpendicular line crosses AB is the midpoint M of the primary diagonal of the rhombus.

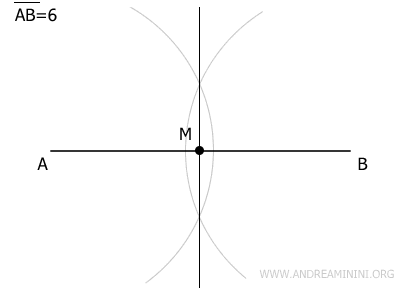
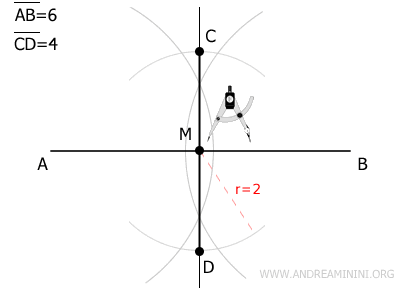
Now, draw the secondary diagonal of the rhombus.

Place the compass point at M and draw an arc with a radius of half the length of the secondary diagonal, or 2 units.

The points where the arc intersects the perpendicular line are the endpoints C and D of the secondary diagonal.

Finally, connect points A, B, C, and D to form the rhombus by drawing segments AC, AD, BC, and BD.

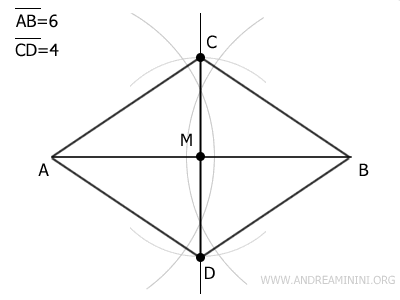
By following these steps, you can create a rhombus, which is a parallelogram with equal sides, perpendicular diagonals, a primary diagonal of 6 units, and a secondary diagonal of 4 units.

Additional Notes

Here are some further observations about the rhombus:

• A parallelogram is a rhombus if it has two consecutive congruent sides

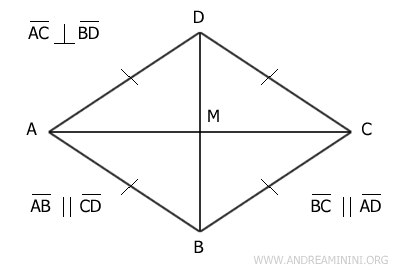
  Proof. Since ABCD is a parallelogram, we know its opposite sides are congruent. Thus, AB≅CD and AD≅BC. If we assume that consecutive sides AB and BC are congruent (AB≅BC), we can deduce by the transitive property that AB≅AD and BC≅CD. Consequently, all sides of the parallelogram are congruent, meaning ABCD is a rhombus.

• The diagonals of a rhombus are perpendicular and bisect the angles

  Proof. Consider a rhombus ABCD where the diagonals intersect at their midpoint M. We need to prove that the diagonals AC and BD are perpendicular and bisect the corresponding angles.
  
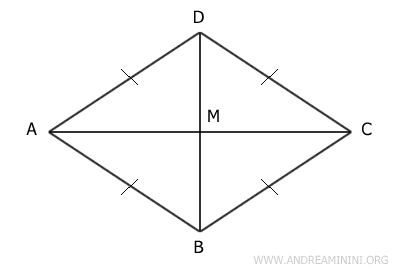
  Since it's a rhombus, all its sides are congruent. This makes triangle ACD an isosceles triangle because sides AD≅CD are congruent. In isosceles triangles, the median is also the height and the angle bisector. Therefore, segment DM is the bisector of angle D. Additionally, segment DM serves as the height, which is perpendicular to side AC (the rhombus's diagonal). The same logic applies to triangle ABC because, according to the third congruence criterion (SSS), it is congruent to triangle ACD, meaning ABC≅ACD. Therefore, diagonal BD is perpendicular to diagonal AC (and vice versa) and bisects the angles at vertices B and D.
  
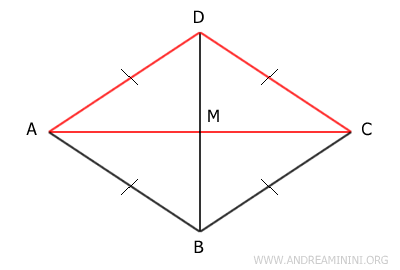
  Now, consider triangle ABD. It is also an isosceles triangle because sides AD≅AB are congruent. Therefore, segment AM is the median, height, and bisector of the angle at vertex A. This shows that it bisects the angle at vertex A and is perpendicular to diagonal BD. The same reasoning applies to triangle BCD, which, according to the third congruence criterion, is congruent to triangle ABD, meaning BCD≅ABD. In conclusion, diagonal AC bisects the angles at vertices A and C and is perpendicular to diagonal BD.
  

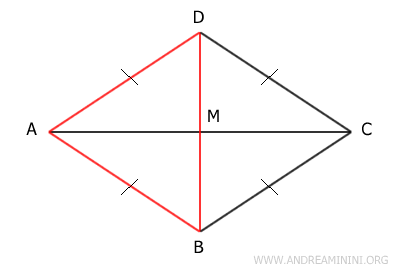
• A parallelogram is a rhombus if its diagonals are perpendicular

  Proof. Let's assume ABCD is a parallelogram with diagonals AC and BD that are perpendicular to each other. Since ABCD is a parallelogram, its diagonals bisect each other at their midpoint M. Therefore, AM is congruent to CM, and BM is congruent to DM.
  
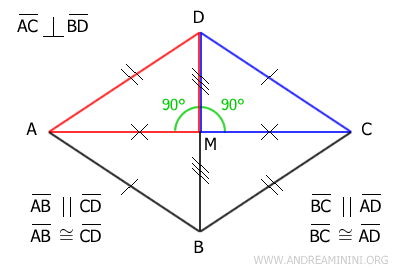
  Knowing that AM≅CM and BM≅DM, right triangles AMD and CMD are congruent (AMD≅CMD) by the first congruence criterion, as they share a common side (DM), have congruent sides AM≅CM, and congruent right angles. Since these two triangles are congruent, all their sides and angles are congruent. Notably, their hypotenuses are congruent (AD≅CD) because they are consecutive sides of the parallelogram. From this, we deduce that all sides of the parallelogram are congruent, making it a rhombus.

• A parallelogram is a rhombus if one diagonal bisects an angle

  Proof. Consider a parallelogram ABCD. Suppose one of its diagonals also bisects an angle, such as diagonal AC bisecting the angle at vertex A. Therefore, angles α'≅α'' are congruent.
  
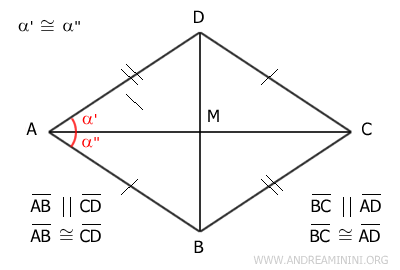
  The opposite sides of a parallelogram are always parallel, so diagonal AC acts as a transversal of the parallel lines AD||BC. According to the parallel lines theorem, alternate interior angles are congruent. Thus, angles α' and γ are congruent (α'≅γ).
  
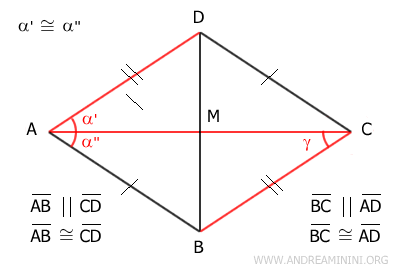
  This indicates that triangle ABC has two congruent angles (α'≅γ) adjacent to side AC, making ABC an isosceles triangle with respect to the base AC. Since it is an isosceles triangle, its oblique sides AB≅BC are congruent. From this, we conclude that the parallelogram is a rhombus because two consecutive sides AB and BC are congruent.

• A diagonal divides the rhombus into two congruent isosceles triangles

  Proof. A rhombus has all sides congruent and diagonals that are perpendicular. Additionally, since it is a parallelogram, the diagonals intersect at their midpoint M. As a result, each diagonal divides the rhombus into two isosceles triangles. For example, diagonal AC divides rhombus ABCD into triangles ACD and ABC. These triangles have two congruent sides: AD≅CD and AB≅BC. Therefore, they are both isosceles triangles. Moreover, by the third congruence criterion (SSS), they are congruent triangles: ACD≅ABC, because all their sides are congruent.
  
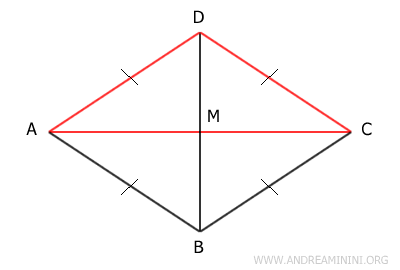
  The other diagonal, BD, also divides the rhombus into two triangles, ABD and BCD. The congruent sides are AB≅AD and BC≅CD. Therefore, both triangles are isosceles. Furthermore, as all three sides are congruent, by the third congruence criterion (SSS), triangles ABD≅BCD are congruent.
  

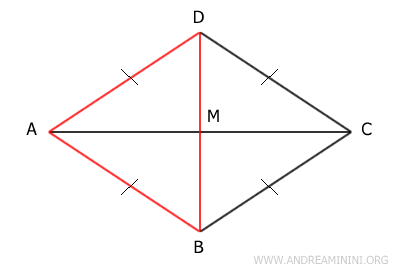
• The diagonals divide the rhombus into four congruent right triangles

  Proof. A rhombus has all sides congruent, and its diagonals are perpendicular to each other. Furthermore, the diagonals intersect at their midpoint M. Therefore, by the third congruence criterion (SSS), triangles AMD≅CDM are congruent because all their sides are congruent. Similarly, triangles ABM≅BCM are congruent.
  
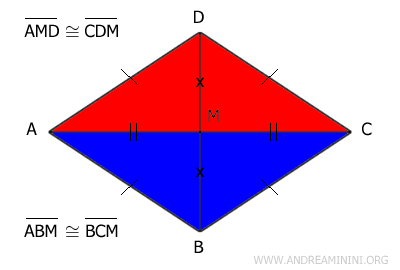
  Additionally, triangles AMD≅ABM are congruent because they share three congruent sides. Thus, by the transitive property, all four right triangles are congruent: AMD≅ABM≅BCM≅CDM.
  

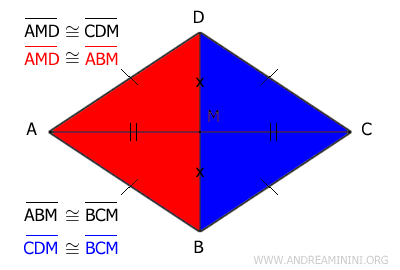
And so on.