Area of a Rhombus

The area of a rhombus can be calculated by multiplying the lengths of its diagonals and then dividing by two: $$ A = \frac{d_1 \cdot d_2}{2} $$

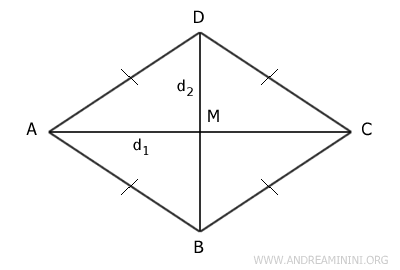
This formula is derived from the fact that the area of a rhombus is equivalent to the area of a right triangle where the base and height correspond to the diagonals of the rhombus.

Inverse Formulas

Given that the area of a rhombus is

$$ A = \frac{d_1 \cdot d_2}{2} $$

You can determine the length of one diagonal by doubling the area and dividing it by the length of the other diagonal:

$$ d_1 = \frac{2A}{d_2} $$

$$ d_2 = \frac{2A}{d_1} $$

A Practical Example

Suppose we have a rhombus with diagonals measuring d₁=3 cm and d₂=4 cm. To find the area of the rhombus, we use the formula:

$$ A = \frac{d_1 \cdot d_2}{2} $$

Substituting the given diagonal lengths:

$$ A = \frac{3 \ cm \cdot 4 \ cm}{2} $$

$$ A = \frac{12 \ cm^2}{2} $$

$$ A = 6 \ cm^2 $$

Therefore, the area of the rhombus is 6 cm².

Proof

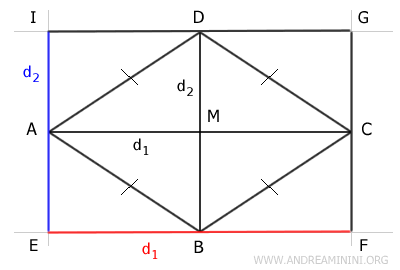
Consider a rhombus ABCD.

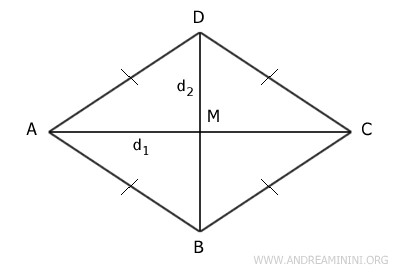
Draw lines through the vertices that are perpendicular to the diagonals.

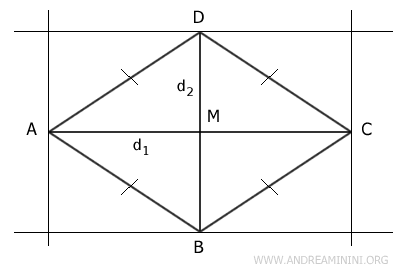
These lines are parallel and form a rectangle, labeled EFGI.

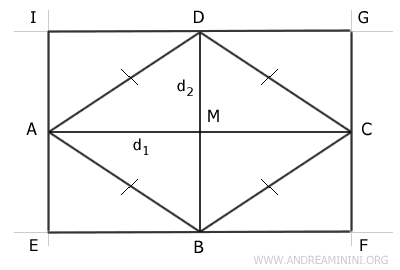
The sides of this rectangle are congruent to the diagonals of the rhombus.

$$ d_1 = \overline{AC} \cong \overline{EF} \cong \overline{GI} $$

$$ d_2 = \overline{BD} \cong \overline{EI} \cong \overline{FG} $$

The area of the rectangle is divided into 8 congruent triangles, while the area of the rhombus is divided into 4 congruent triangles.

Thus, to find the area of the rhombus, you can simply calculate the area of the rectangle (base times height) and then divide the result by two.

In other words, the area of the rhombus is half the area of the rectangle.

$$ A = \frac{b \cdot h}{2} $$

Since the sides of the rectangle are congruent to the diagonals of the rhombus, with b=d₁ and h=d₂, this means you need to multiply the diagonals of the rhombus and divide the product by two.

$$ A = \frac{d_1 \cdot d_2}{2} $$

This explains the formula used to calculate the area of a rhombus.

Observations

Here are a few observations about the area of a rhombus:

• A rhombus is a parallelogram with congruent sides. Therefore, its area can also be calculated using the parallelogram formula: base times height divided by two. $$ A = \frac{b \cdot h}{2} $$
• A square is a special type of rhombus where the diagonals are congruent. Therefore, you can calculate the area of a square using the rhombus formula: $$ A = \frac{d \cdot d}{2} = \frac{d^2}{2} $$ From this, you can find the diagonal length of the square using $$ d^2 = 2A $$ Taking the square root of both sides gives us $$ \sqrt{d^2}=\sqrt{2A} $$ So $$ d=\sqrt{2A} $$

And so on.