Exterior Angle Sum Theorem for Convex Polygons

In any convex polygon with $n$ sides, the sum of the exterior angles (one per vertex) is always equal to a full rotation (360°).

In other words, the sum of the exterior angles of a convex polygon remains constant - it does not depend on the number of sides or the specific shape of the polygon. In this sense, it is an important invariant.

For instance, whether it’s a triangle, a square, a pentagon, or any polygon with n sides, the sum of the exterior angles will always be 360°.

Example: Imagine you’re walking along the edge of a fence. The exact shape of the fence doesn’t matter - it could have many angles or just a few. The only condition is that it must be a convex polygon. Every time you reach a corner, you change direction.

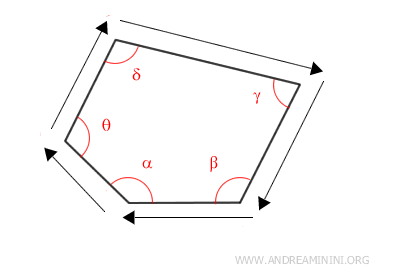
The total of all these direction changes as you walk around the fence is exactly 360°, just as if you had made a complete circle around it.

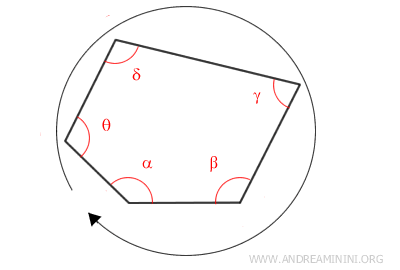
The Proof

Let’s consider a convex polygon.

For example, a convex polygon with n = 5 sides.

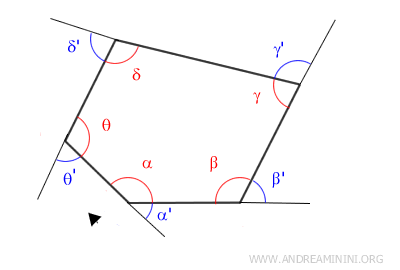
Each exterior angle of a convex polygon is adjacent to an interior angle.

Therefore, each exterior angle is supplementary to its adjacent interior angle, together forming a straight angle of 180°.

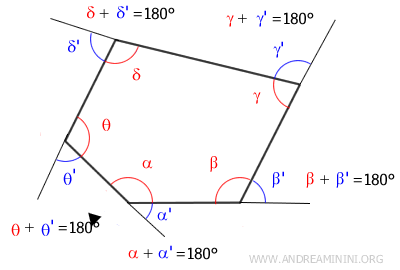
This means that in a convex polygon with n sides, there are n pairs of angles, and the sum of the interior and exterior angles together is n × 180°.

$$ n \cdot 180° $$

Knowing that the sum of the interior angles is equal to (n-2) × 180°, we can calculate the sum of the exterior angles by subtracting this from the total.

In essence, the sum of the exterior angles is equal to the total of both the interior and exterior angles minus the sum of the interior angles.

Thus, the sum of the exterior angles of a convex polygon is:

$$ n \cdot 180° - [ (n-2) \cdot 180° ] $$

With a bit of simple algebra, this simplifies to:

$$ [ n - (n-2) ] \cdot 180° = $$

$$ ( n - n + 2 ) \cdot 180° = $$

$$ 2 \cdot 180° = 360° $$

So, no matter how many sides a convex polygon has, the sum of its exterior angles will always be 360°.

And that’s the theorem!

Notes

Here are a few key points about the sum of the exterior angles of a convex polygon:

• The exterior angle sum is a stronger invariant than the interior angle sum
  The sum of the exterior angles of any convex polygon is always 360°, provided you take exactly one exterior angle at each vertex - regardless of how many sides the polygon has or what shape it takes. In contrast, the sum of the interior angles depends on the number of sides $ n $ and is given by $ (n-2) \cdot 180° $. As such, it is a weaker invariant, because it varies as $ n $ changes.

And so on.