External Angles

External angles are formed by the intersection of one side of a polygon and the extension of an adjacent side.

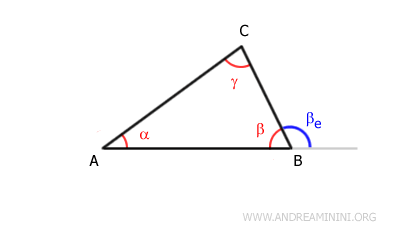
For example, consider triangle ABC.

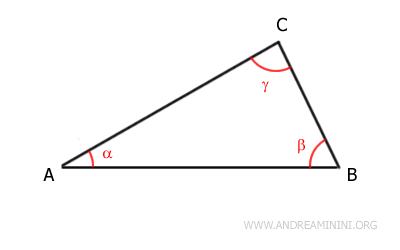
The triangle has three internal angles: α, β, and γ.

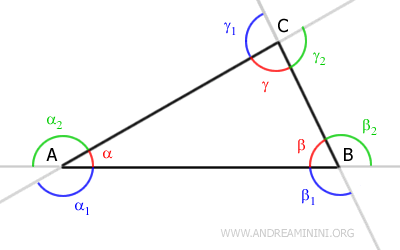
The triangle has the following external angles measured counterclockwise:

• Angle α₁ is between the extension of side AC and side AB.
• Angle α₂ is between side AC and the extension of side AB.
• Angle β₁ is between side AB and the extension of side BC.
• Angle β₂ is between the extension of side AB and side BC.
• Angle γ₁ is between the extension of side BC and side AC.
• Angle γ₂ is between side BC and the extension of side AC.

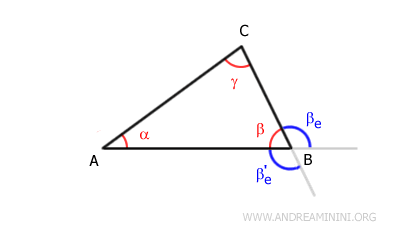
Each internal angle has two adjacent external angles. For example, the internal angle β has two adjacent external angles: β_e and β_e'.

Observations

Some useful observations about the sum of angles:

• Sum of external angles
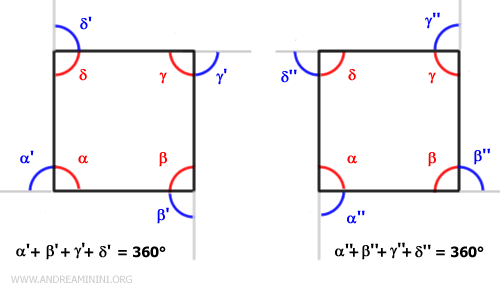
  The sum of the external angles of a polygon is always 360°, regardless of the number of sides.

  Example: A square has 4 sides and 4 internal angles of 90°. Although each angle has two adjacent external angles, we only consider 4 external angles at a time, one at each vertex. The sum of these external angles is always 360°.
  

• External Angle Theorem
  In a triangle, each external angle is greater than either of the non-adjacent internal angles.

  Example: In triangle ABC, the external angle β_e is greater than each of the internal angles that are not adjacent to it: α and γ.
  
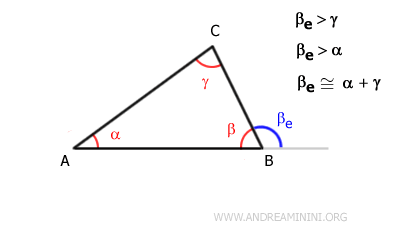
  The internal angle β is not considered because it is adjacent to the external angle β_e.

• Relationship between internal and external angles
  In any polygon, the sum of an internal angle and its adjacent external angle is always equal to a straight angle of 180°.

  Example: In triangle ABC, the sum of the internal angle β and the external angle β_e forms a straight angle (180°).
  

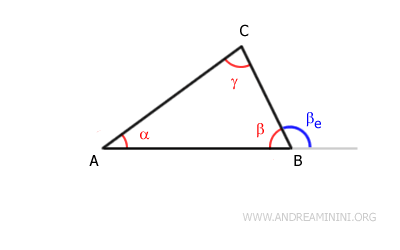
And so on.