Area of a Parallelogram

The formula to calculate the area of a parallelogram is: $$ A = b \times h $$ where $ A $ represents the area, $ b $ is the length of the base, and $ h $ is the height, which is the perpendicular distance between the base and the opposite side.

The concept of the parallelogram’s area dates back to ancient Greek mathematicians like Euclid, who described various properties of parallelograms and other geometric figures in his famous book, "Elements."

A Practical Example
Explanation
Calculating Area Using Cartesian Coordinates

A Practical Example

Let’s consider a parallelogram with a base of 5 meters and a height of 3 meters.

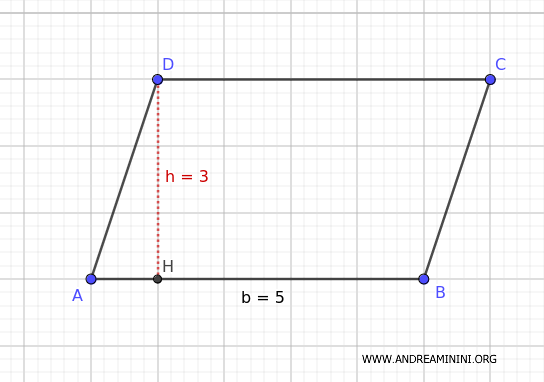
example

The area of the parallelogram is:

$$ A = 5 \, m \times 3 \, m = 15 \, m^2 $$

Explanation

To understand how this formula works, imagine transforming the parallelogram into a rectangle.

Draw the height inside the parallelogram, passing through vertex D.

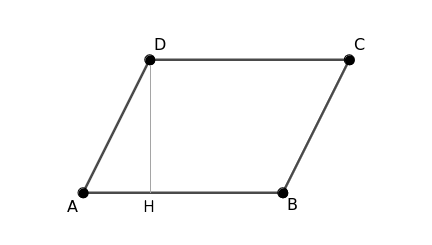
example

Now, cut along the triangle ADH and move it to the opposite side.

This creates a rectangle HDCE that has the same base and height as the original parallelogram.

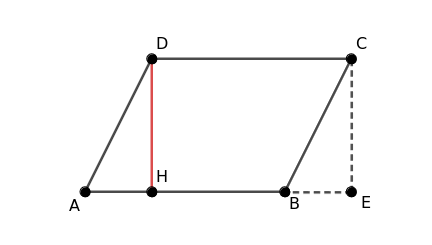
equivalent rectangle

So, a parallelogram is equivalent to a rectangle with the same base and height.

Since the area of a rectangle is calculated by multiplying the base by the height, the same method applies to a parallelogram.

Calculating Area Using Cartesian Coordinates

An alternative method for finding the area of a parallelogram is by using the Cartesian coordinates of its vertices.

If the vertices of the parallelogram are given by the points $ (x_1, y_1) $, $ (x_2, y_2) $, $ (x_3, y_3) $, and $ (x_4, y_4) $, the area can be calculated using the determinant of the coordinates:

$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right| $$

Example

Let’s walk through an example of calculating the area of a parallelogram using the Cartesian coordinates of its vertices.

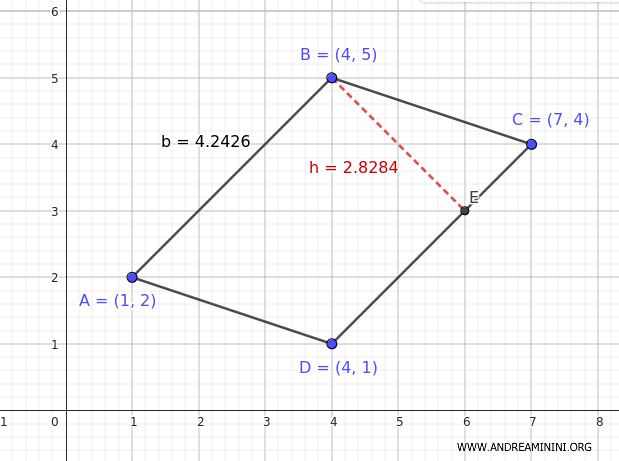
Suppose we have a parallelogram with vertices at the following coordinates:

$$ A (1, 2) $$

$$ B (4, 5) $$

$$ C (7, 4) $$

$$ D (4, 1) $$

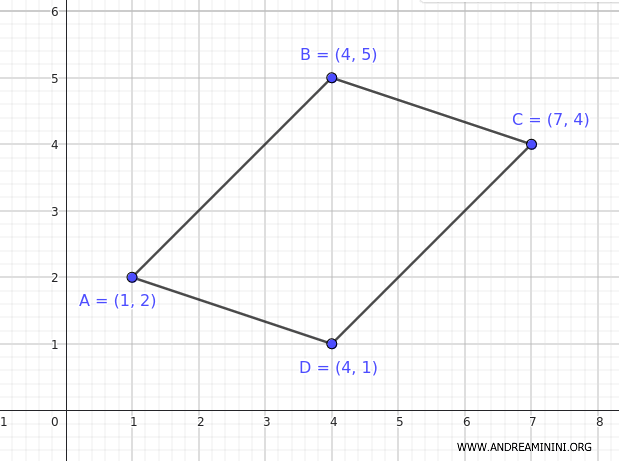
vertex coordinates of the parallelogram

We list the coordinates in cyclic order:

$$ (x_1, y_1) = (1, 2) \\
(x_2, y_2) = (4, 5) \\
(x_3, y_3) = (7, 4) \\
(x_4, y_4) = (4, 1) $$

Now, we apply the determinant formula:

$$ A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right| $$

Substituting the coordinates into the formula:

$$ A = \frac{1}{2} \left| 1 \cdot 5 + 4 \cdot 4 + 7 \cdot 1 + 4 \cdot 2 - (2 \cdot 4 + 5 \cdot 7 + 4 \cdot 4 + 1 \cdot 1) \right| $$

We calculate the individual products:

$$ A = \frac{1}{2} \left| 5 + 16 + 7 + 8 - (8 + 35 + 16 + 1) \right| $$

$$ A = \frac{1}{2} \left| 36 - 60 \right| $$

$$ A = \frac{1}{2} \left| -24 \right| $$

$$ A = \frac{1}{2} \cdot 24 $$

$$ A = 12 $$

The area of the parallelogram with vertices at the coordinates $ (1, 2) $, $ (4, 5) $, $ (7, 4) $, and $ (4, 1) $ is $ 12 \, \text{square units} $.

In fact, if you calculate the area of the parallelogram using the formula $ A = b \cdot h $, you also get A = 12.

$$ A = b \cdot h = 4.2426 \cdot 2.8284 = 12 $$

parallelogram area

And so on.