Difference Between Congruence and Equality

The terms "congruence" and "equality" are often used interchangeably, but in mathematics and geometry, they have distinct meanings.

• Equality
  

  Two geometric figures are considered equal if they match exactly, point for point, without the need for any rigid transformation.

  Therefore, two equal figures perfectly overlap in space, sharing the same shape, size, and position. In geometry, equality is represented by the equal sign "=" $$ A=B $$

  For example, the height and the median of an isosceles triangle are equal because they coincide point for point. Here's an example of equal figures:
  

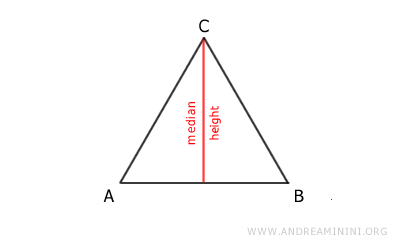
• Congruence
  

  Two geometric figures are called "congruent" if they correspond exactly, point by point, after a rigid transformation (e.g., rotation, reflection, translation).

  As a result, congruent figures have the same shape and size but occupy different positions in space. In geometry, congruence is represented by the symbol for "approximately equal," which is an equal sign with a tilde above it ≅ $$ A≅B $$

  For example, the sides AB and BC of an isosceles triangle are congruent because they can be made to overlap after a rotation and translation.
  

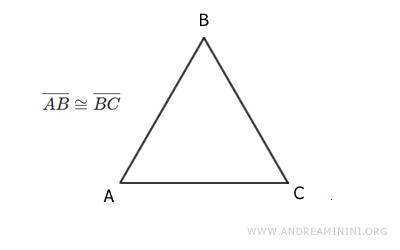
In summary, congruence is a broader concept than equality in geometry, allowing figures with identical shapes and sizes to occupy different positions in space.

In both cases, the figures have the same shape and size but differ in their positions.

And so on.