Side of a Hexagon and the Radius of the Inscribed Circle

The side length (l) of a regular hexagon is related to the radius (r) of the inscribed circle by the following formula: $$ l = \frac{2 \sqrt{3}}{3} \cdot r $$

The radius of the inscribed circle, which is the same as the apothem of the hexagon, shares the same relationship with the side length (a) of the hexagon.

$$ l = \frac{2 \sqrt{3}}{3} \cdot a  $$

This latter formula is more commonly known, but it’s essentially identical to the previous one.

Inverse Formulas. Similarly, you can calculate the radius (r) of the inscribed circle from the side length (l) of the hexagon using the inverse formula: $$ r = l \cdot \frac{3}{2 \sqrt{3}} = l \cdot \frac{\sqrt{3} }{2} $$ or for the apothem: $$ a = l \cdot \frac{3}{2 \sqrt{3}} = l \cdot \frac{\sqrt{3} }{2} $$

A Practical Example

Let’s consider a regular hexagon with sides of length 2 and an inscribed circle with radius r = 1.7321.

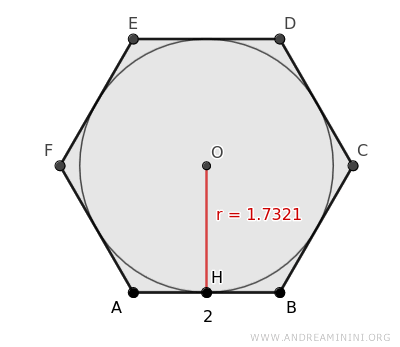
We can use the formula to calculate the side length based on the radius of the inscribed circle:

$$ l = \frac{2 \sqrt{3}}{3} \cdot r $$

In this case, the radius is r = 1.7321

$$ l = \frac{2 \sqrt{3}}{3} \cdot 1.7321 $$

By performing the calculations, we find the exact side length of the hexagon:

$$ l = 2 $$

Here, the radius (r) is also the apothem (a) of the hexagon.

The Proof

Consider a hexagon with an inscribed circle centered at O and with radius r.

The center of the inscribed circle is also the center of the regular hexagon because it’s the point where the diagonals intersect.

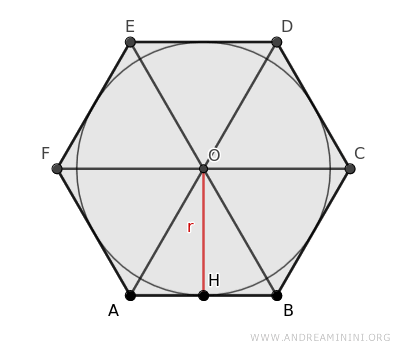
The diagonals divide the hexagon into six triangles, each dividing the central angle into six equal parts of 360°/6 = 60°.

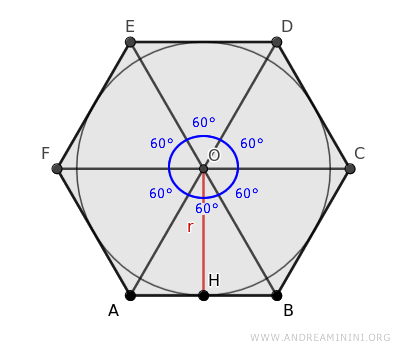
These triangles are congruent because, according to the criteria for triangle congruence, they have two congruent sides and a congruent angle between them (60°).

This allows us to focus on just one of these triangles, such as triangle ABO.

The diagonals divide the internal angles of the hexagon (120°) into two congruent angles of 60° each.

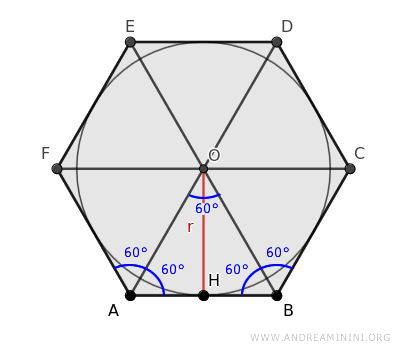
This means that triangle ABO has all angles equal to 60° and is therefore an equilateral triangle.

Now, we need to find the relationship between the radius (r) of the inscribed circle and the side length (l) of the hexagon.

The radius r splits the equilateral triangle ABO into two right triangles, AHO and BHO.

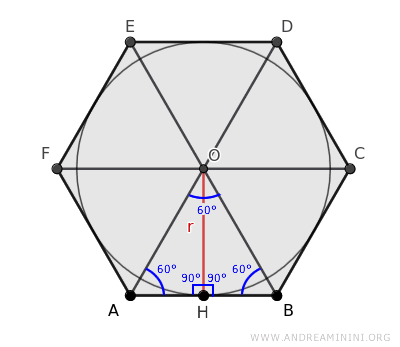
We can then use Pythagoras' theorem on one of the right triangles to calculate the length of the leg OH (radius r).

For example, let's apply Pythagoras' theorem to triangle AHO:

$$ \overline{OH} = \sqrt{\overline{AO}^2 - \overline{AH}^2} $$

The segment OH corresponds to the radius r of the inscribed circle:

$$ r = \sqrt{\overline{AO}^2 - \overline{AH}^2} $$

The segment AO is congruent to the side of the hexagon (l) because triangle ABO is equilateral.

$$ r = \sqrt{l^2 - \overline{AH}^2} $$

The segment AH is half the length of the hexagon's side (l/2).

$$ r = \sqrt{l^2 - ( \frac{l}{2} )^2} $$

Let’s work through the algebra:

$$ r = \sqrt{l^2 - \frac{l^2}{4} } $$

$$ r = \sqrt{ \frac{4l^2-l^2}{4} } $$

$$ r = \sqrt{ \frac{3l^2}{4} } $$

$$ r = \frac{l}{2} \sqrt{ 3 } $$

Now we can solve for the side length:

$$ r \cdot \frac{ 2 }{ \sqrt{3} } = \frac{l}{2} \sqrt{ 3 } \cdot \frac{ 2 }{ \sqrt{3} } $$

$$ r \cdot \frac{ 2 }{ \sqrt{3} } = l $$

To remove the square root from the denominator, multiply and divide the fraction on the left side by the square root of three:

$$ r \cdot \frac{ 2 }{ \sqrt{3} } \cdot \frac{\sqrt{3}}{\sqrt{3}} = l $$

$$ r \cdot \frac{ 2 \sqrt{3} }{ \sqrt{3} \cdot \sqrt{3} } = l $$

$$ r \cdot \frac{ 2 \sqrt{3} }{ \sqrt{3 \cdot 3} } = l $$

$$ r \cdot \frac{ 2 \sqrt{3} }{ \sqrt{3^2} } = l $$

$$ r \cdot \frac{ 2 \sqrt{3} }{ 3 } = l $$

Finally, we can rearrange the terms:

$$ l = \frac{ 2 \sqrt{3} }{ 3 } \cdot r $$

This proves the existence of the formula that relates the radius (r) of the inscribed circle to the side length (l) of a regular hexagon.

Note. Knowing that the radius of the inscribed circle is the same as the apothem of a regular hexagon (r = a), we can also write the formula in this equivalent form: $$ l = \frac{ 2 \sqrt{3} }{ 3 } \cdot a $$

And so on.