Diagonal of a Square

The length of a square's diagonal (d) is equal to the length of one side (l) multiplied by the square root of 2: $$ d = l \cdot \sqrt{2} $$

The ratio between the diagonal and the side remains constant for all squares, regardless of their size.

$$ \frac{d}{l} = \sqrt{2} $$

This relationship makes it easy to calculate the diagonal if you know the side length, or vice versa.

Example

Let’s take a square with a side length of 4.

$$ l = 4 $$

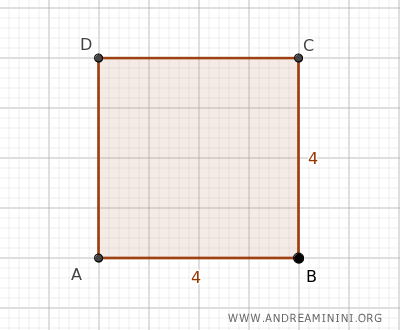
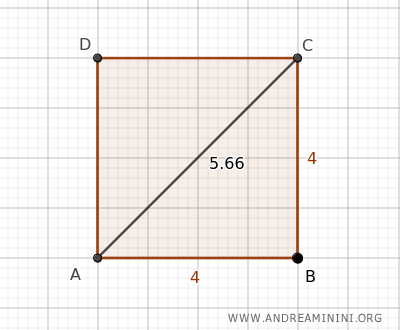
The length of its diagonal is:

$$ d = l \cdot \sqrt{2} $$

$$ d = 4 \cdot \sqrt{2} $$

$$ d = 5.66 $$

So, the diagonal of the square is approximately 5.66 units long.

Proof

This result can be proven using the Pythagorean theorem.

The diagonal divides the square into two isosceles right triangles.

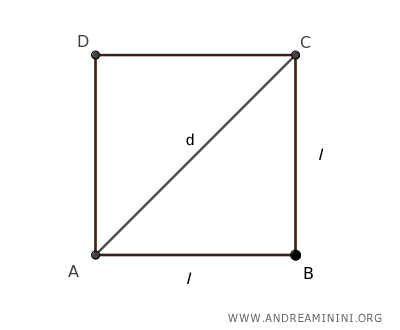
In each triangle, the legs are the sides of the square (l), and the hypotenuse is the diagonal (d).

The Pythagorean theorem tells us that in a right triangle, the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides.

$$ d^2 = l^2 + l^2 $$

Simplifying, we get:

$$ d^2 = 2 \cdot l^2 $$

Taking the square root of both sides and simplifying further, we have:

$$ \sqrt{ d^2 } = \sqrt{ 2 \cdot l^2 } $$

$$ d = l \cdot \sqrt{2} $$

This gives us the formula we set out to prove.

Observations

Here are a few additional notes and observations on the diagonal of a square:

• The diagonal and the side of a square are incommensurable
  The diagonal and the side of a square are incommensurable, meaning they do not share a common divisor.

  Proof. Consider a square ABCD.
  
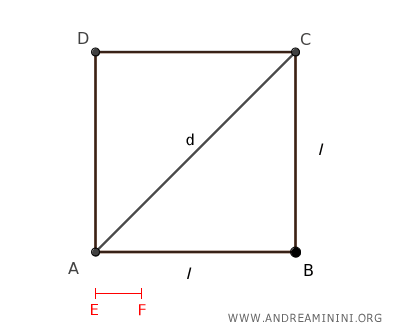
  Suppose, for the sake of argument, that the side AB and the diagonal AC are commensurable. This would imply that there exists a common unit EF, which divides evenly into the diagonal AC m times and into the side AB n times: $$ \overline{AC} = m \cdot \overline{EF} $$ $$ \overline{AB} = n \cdot \overline{EF} $$ By the Pythagorean theorem, in the right triangle ABC, the square of the hypotenuse equals the sum of the squares of the legs: $$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 $$ Since in a square all sides are equal, AB = BC: $$ \overline{AC}^2 = \overline{AB}^2 + \overline{AB}^2 $$ $$ \overline{AC}^2 = 2 \cdot \overline{AB}^2 $$ Substituting AC = m · EF and AB = n · EF, we get: $$ (m \cdot \overline{EF})^2 = 2 \cdot (n \cdot \overline{EF})^2 $$ $$ m^2 \cdot \overline{EF}^2 = 2 \cdot n^2 \cdot \overline{EF}^2 $$ Simplifying by canceling out EF² from both sides: $$ m^2 = 2 \cdot n^2 $$ Here, m and n are integers. However, this equation has no solutions because the left side and the right side would need to be factorizable into the same prime factors. Yet, the right side has an extra factor of 2. Thus, the equation has no solutions where n ≠ 0, meaning no pair of non-zero integers (m, n) exists such that m² = 2n². Since this leads to a contradiction, our initial assumption that the diagonal and the side of the square are commensurable must be false. Therefore, the diagonal and the side of a square are indeed incommensurable.

And so on.