Relationship Between the Side of a Square and the Radius of Its Circumscribed Circle

There's a direct relationship between the side length of a square and the radius of a circumscribed circle that passes through all the square’s vertices:

• The side length of the square is equal to the radius of the circumscribed circle multiplied by the square root of two. $$ l = r \cdot \sqrt{2} $$
  
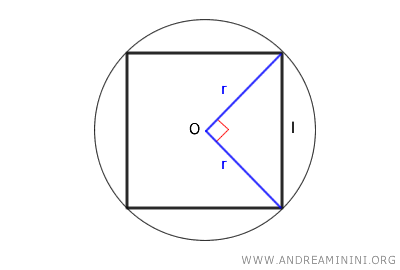
• The side length of the square is also equal to twice the radius (2r) of the circumscribed circle (which is also the diagonal of the square) divided by the square root of two. $$ l = \frac{2r}{\sqrt{2}} = \frac{d}{\sqrt{2}} $$

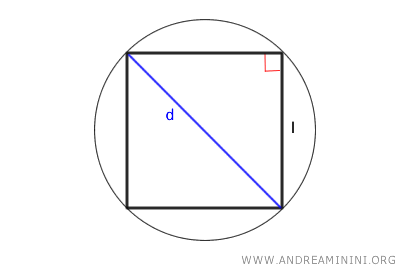
A Practical Example

In this example, the square has a side length of 3, and the radius of the circumscribed circle is r = 2.1213.

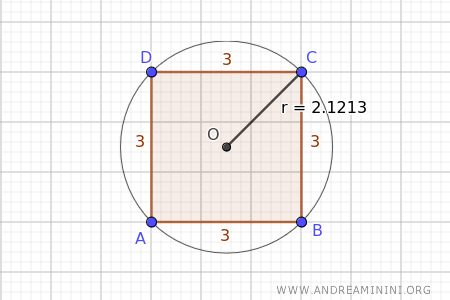
Let’s verify the relationship between the side length of the square and the radius of the circumscribed circle using the first formula:

$$ l = r \cdot \sqrt{2} $$

$$ 3 = 2.1213 \cdot \sqrt{2} = 3 $$

The equation holds true.

Now, let’s verify the same relationship using the second formula:

$$ l = \frac{2r}{\sqrt{2}} $$

$$ l = \frac{2 \cdot 2.1213}{\sqrt{2}} = 3 $$

Again, the equation is confirmed.

The Proof

We can break down the proof into two parts, one for each formula.

1] First Formula

Consider a square and its circumscribed circle.

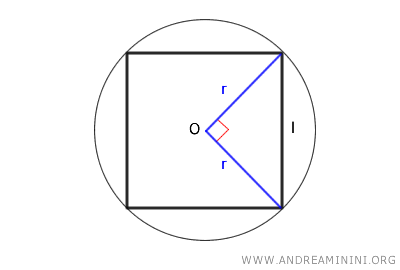
The radii of the circle that connect the center (O) to the endpoints of one side of the square form a right triangle, where the side of the square is the hypotenuse and the radii are the legs.

Using Pythagoras' theorem, we can calculate the hypotenuse from the lengths of the legs:

$$ l = \sqrt{r^2 + r^2} $$

$$ l = \sqrt{2r^2} $$

$$ l = r \cdot \sqrt{2} $$

This proves the first formula.

2] Second Formula

The diagonal of a square is found by multiplying the side length of the square by the square root of two:

$$ d = l \cdot \sqrt{2} $$

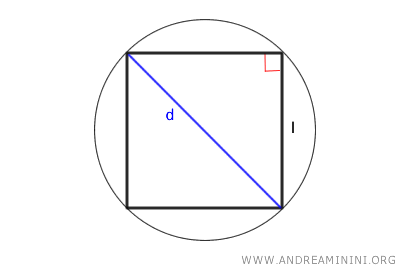
Since the diagonal is equal to twice the radius, d = 2r, we can derive the side length from the radius:

$$ 2r = l \cdot \sqrt{2} $$

Thus, the side length (l) of the square is equal to the radius (r) of the circumscribed circle multiplied by two and divided by the square root of two:

$$ l = \frac{2r}{\sqrt{2}} $$

Alternative Proof. This formula can also be derived by a straightforward algebraic manipulation of the formula relating the side length to the radius. Starting with $$ l = r \cdot \sqrt{2} $$ we can multiply and divide by the square root of two: $$ l = r \cdot \sqrt{2} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$ This simplifies to: $$ l = \frac{r \cdot \sqrt{2} \cdot \sqrt{2}}{\sqrt{2}} $$ $$ l = \frac{r \cdot 2}{\sqrt{2}} $$

And so on.