Area of a Quadrilateral with Perpendicular Diagonals

The area \( A \) of a quadrilateral with perpendicular diagonals \( d_1 \) and \( d_2 \) can be calculated using the following formula: $$ A = \frac{d_1 \cdot d_2}{2} $$

In other words, if a quadrilateral has perpendicular diagonals, you can find its area by multiplying the lengths of the diagonals and dividing the result by 2.

This formula comes from the fact that when the diagonals are perpendicular, the quadrilateral can be divided into four right triangles.

Inverse Formulas: The inverse formulas allow you to determine the length of one diagonal when you know the area of the quadrilateral and the length of the other diagonal. From the area formula, we can derive: $$ d_1 = \frac{2A}{d_2} $$ and similarly, $$ d_2 = \frac{2A}{d_1} $$ These formulas are particularly useful when you know the area of a quadrilateral and one of its diagonals, and you need to find the length of the other diagonal.

The Proof

Generally speaking, a quadrilateral is a plane figure made up of four sides of varying lengths.

However, within the category of quadrilaterals, there are specific shapes like rectangles, rhombuses, and squares that have unique properties related to their diagonals.

For example, in the case of a rhombus, you can calculate the area by multiplying the lengths of the longer and shorter diagonals and dividing by two. This property doesn't only apply to rhombuses with equal sides but to all quadrilaterals with perpendicular diagonals.

Quadrilaterals with perpendicular diagonals allow you to calculate the area using the lengths of the diagonals.

When the diagonals of a quadrilateral are perpendicular to each other, they intersect at right angles.

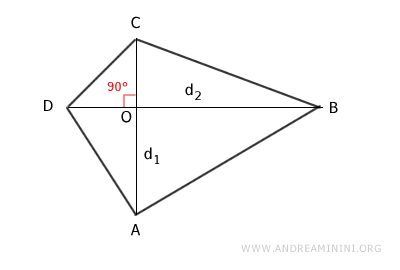
As a result, the area of the quadrilateral can be divided into four right triangles: ODC, OAD, OBC, and OAB.

The total area of the quadrilateral is found by summing the areas of these four triangles:

$$ A = A_{ODC} + A_{OAD} + A_{OBC} + A_{OAB} $$

The area of each triangle is calculated by multiplying the base by the height and dividing by two:

$$ A= \frac{ \overline{OD} \cdot \overline{OC} }{2} + \frac{ \overline{OD} \cdot \overline{OA} }{2} + \frac{ \overline{OB} \cdot \overline{OC} }{2} + \frac{ \overline{OB} \cdot \overline{OA} }{2} $$

This simplifies to:

$$ A= \frac{ \overline{OD} \cdot \overline{OC} + \overline{OD} \cdot \overline{OA} + \overline{OB} \cdot \overline{OC} + \overline{OB} \cdot \overline{OA} }{2} $$

Further simplifying, we get:

$$ A= \frac{ \overline{OD} \cdot (\overline{OC} + \overline{OA}) + \overline{OB} \cdot (\overline{OC} + \overline{OA}) }{2} $$

Knowing that diagonal d₁ = OC + OA,

$$ A= \frac{ \overline{OD} \cdot d_1 + \overline{OB} \cdot d_1 }{2} $$

This can be rewritten as:

$$ A= \frac{ d_1 \cdot (\overline{OD} + \overline{OB}) }{2} $$

Since diagonal d₂ = OD + OB,

$$ A= \frac{ d_1 \cdot d_2 }{2} $$

The final result is the formula we set out to prove.

The area of a quadrilateral with perpendicular diagonals is equal to the product of the diagonals divided by two.

And that’s how it’s done.