Standard Form Equation of a Parabola Parallel to the y-axis
The standard form equation of a parabola with vertex \((h, k)\) and an axis of symmetry parallel to the \(y\)-axis is $$ (x - h)^2 = 4p(y - k) $$. Here, $ p $ is the distance from the focus \((x_F, y_F) \) to the vertex \((h, k)\). $$ p = y_F - k $$
This equation stems from the geometric definition of a parabola as the set of all points equidistant from a fixed point (the focus) and a fixed line (the directrix).
The value of $ p $ determines the direction the parabola opens:
- If $ p>0 $, the parabola opens upward.
- If $ p<0 $, the parabola opens downward.
This form is particularly useful because it clearly shows the vertex's position and the distance from the vertex to the focus, making it easier to analyze the parabola.
A Practical Example
The focus of a parabola is at the coordinates \( F(3,2) \), and the vertex is at \( V(3,1) \).
This is a parabola with an axis of symmetry parallel to the y-axis because the focus and vertex share the same x-coordinate, \( x=3 \).
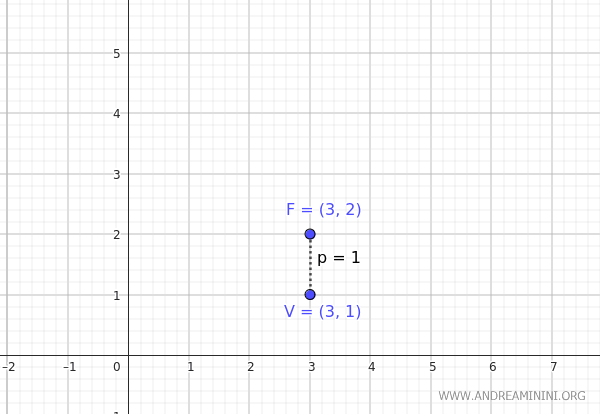
To determine the equation of the parabola, we use the standard form formula:
$$ (x - h)^2 = 4p(y - k) $$
In this case, the distance from the vertex to the focus is \( p = 2 - 1 = 1 \)
$$ (x - h)^2 = 4 \cdot 1 (y - k) $$
$$ (x - h)^2 = 4(y - k) $$
The coordinates of the vertex are \( h = 3 \) and \( k = 1 \)
$$ (x - 3)^2 = 4(y - 1) $$
$$ x^2 - 6x + 9 = 4y - 4 $$
Thus, the equation of the parabola is
$$ y = \frac{x^2}{4} - \frac{3x}{2} + \frac{13}{4} $$
This way, we have derived the equation of the parabola from its focus and vertex.
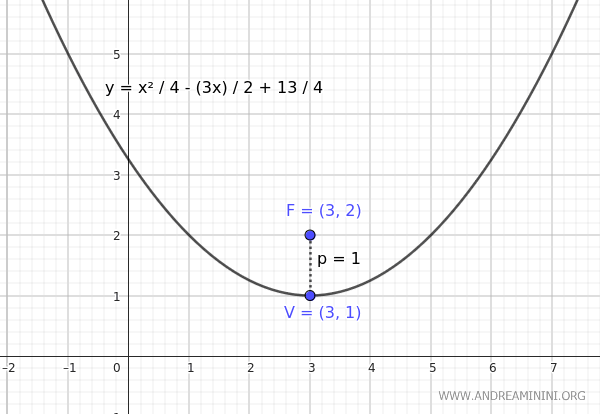
Verification
In the equation of a parabola, the distance between the focus \( F \) and any point \( P \) on the parabola is always equal to the distance between the same point \( P \) and the directrix.
Once we know the quadratic equation of the parabola, we can calculate the equation of the directrix:
$$ y = - \frac{1 + \Delta}{4a} $$
Where \( \Delta = b^2 - 4ac \) is the discriminant of the parabola's equation \( y = \frac{x^2}{4} - \frac{3x}{2} + \frac{13}{4} \)
The coefficients of the equation are \( a = \frac{1}{4} \), \( b = -\frac{3}{2} \), and \( c = \frac{13}{4} \)
$$ \Delta = b^2 - 4ac $$
$$ \Delta = \left(-\frac{3}{2}\right)^2 - 4 \cdot \frac{1}{4} \cdot \frac{13}{4} $$
$$ \Delta = \frac{9}{4} - \frac{13}{4} $$
$$ \Delta = \frac{9 - 13}{4} $$
$$ \Delta = \frac{-4}{4} $$
$$ \Delta = -1 $$
Therefore, the equation of the directrix of the parabola is
$$ y = - \frac{1 + \Delta}{4a} $$
$$ y = - \frac{1 - 1}{4 \cdot \frac{1}{4}} $$
$$ y = 0 $$
In this case, the directrix coincides with the x-axis.
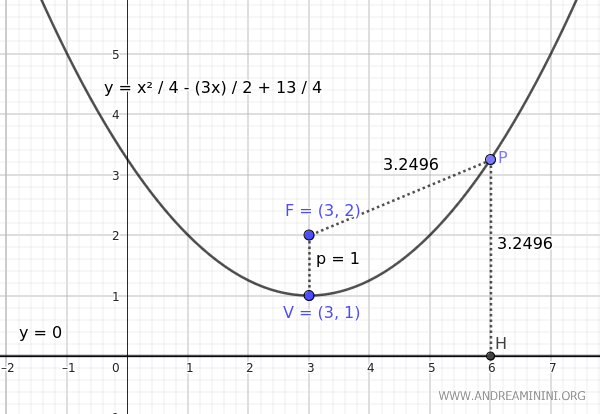
For any point \( P \) on the parabola, the distance between the point and the focus is equal to the distance between the point and the directrix (PF ≈ PH).
Therefore, the equation of the parabola is correct.
Note: In this example, I have performed all the calculations to find the directrix. I did this for completeness, but it is not necessary. You can reach the same result much more easily by considering that the directrix is perpendicular (90°) to the axis of symmetry of the parabola (which in this case is parallel to the y-axis) and is at the same distance from the vertex \( V \) as the distance between the vertex \( V \) and the focus \( F \) but in the opposite direction. In this case, the distance between the vertex and the focus is VF = 1, and the vertex \( V \) is at coordinates (3,1), so we can deduce that the directrix passes through the point (3,0) and is \( y = 0 \) without any calculation.
The Proof
A parabola is the set of points such that the distance from a fixed point, called the focus \((h, k + p)\), is equal to the distance from a fixed straight line, called the directrix \( y = k - p \).
The distance from a point on the parabola \( P(x, y) \) to the focus \((h, k + p)\) is
$$ \sqrt{(x - h)^2 + (y - (k + p))^2} $$
The distance from the same point \( P(x, y) \) to the directrix \( y = k - p \) is
$$ |y - (k - p)| $$
According to the definition of a parabola, these two distances are equal:
$$ \sqrt{(x - h)^2 + (y - (k + p))^2} = |y - (k - p)| $$
Since distance is always positive, we can rewrite the distance from the directrix without the absolute value:
$$ \sqrt{(x - h)^2 + (y - (k + p))^2} = y - (k - p) $$
Squaring both sides, we get:
$$ \left( \sqrt{(x - h)^2 + (y - (k + p))^2} \right)^2 = \left( y - (k - p) \right)^2 $$
$$ (x - h)^2 + (y - (k + p))^2 = (y - (k - p))^2 $$
$$ (x - h)^2 + (y - k - p)^2 = (y - k + p)^2 $$
Now, expanding the squares:
$$ (x - h)^2 + (y - k - p)^2 = (y - k + p)^2 $$
$$ (x - h)^2 + (y - k)^2 - 2p(y - k) + p^2 = (y - k)^2 + 2p(y - k) + p^2 $$
Canceling the common terms on both sides, we get:
$$ (x - h)^2 = 4p(y - k) $$
Thus, the standard form equation of a parabola with a vertex at \((h, k)\) and an axis of symmetry parallel to the y-axis is:
$$ (x - h)^2 = 4p(y - k) $$
Where \( p \) is the distance from the vertex to the focus, and \( 4p \) is a constant that determines the parabola's width.
The larger \( p \), the wider the parabola; the smaller \( p \), the narrower the parabola.
In conclusion, the standard form \((x - h)^2 = 4p(y - k)\) directly derives from the geometric definition of the parabola and the relationship between the focus and the directrix.
And so forth.
